
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,将它的纵坐标
,将它的纵坐标![]() 与横坐标
与横坐标![]() 的比
的比![]() 称为点
称为点![]() 的“理想值”,记作
的“理想值”,记作![]() .如
.如![]() 的“理想值”
的“理想值”![]() .
.
(1)①若点![]() 在直线
在直线![]() 上,则点
上,则点![]() 的“理想值”
的“理想值”![]() 等于_______;
等于_______;
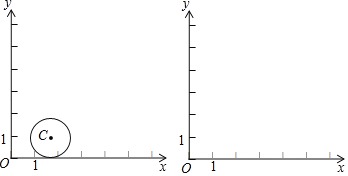
②如图,![]() ,
,![]() 的半径为1.若点
的半径为1.若点![]() 在
在![]() 上,则点
上,则点![]() 的“理想值”
的“理想值”![]() 的取值范围是_______.
的取值范围是_______.
(2)点![]() 在直线
在直线![]() 上,
上,![]() 的半径为1,点
的半径为1,点![]() 在
在![]() 上运动时都有
上运动时都有![]() ,求点
,求点![]() 的横坐标
的横坐标![]() 的取值范围;
的取值范围;
(3)![]() ,
,![]() 是以
是以![]() 为半径的
为半径的![]() 上任意一点,当
上任意一点,当![]() 时,画出满足条件的最大圆,并直接写出相应的半径
时,画出满足条件的最大圆,并直接写出相应的半径![]() 的值.(要求画图位置准确,但不必尺规作图)
的值.(要求画图位置准确,但不必尺规作图)
【答案】(1)①﹣3;②![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)①把Q(1,a)代入y=x-4,可求出a值,根据理想值定义即可得答案;②由理想值越大,点与原点连线与![]() 轴夹角越大,可得直线
轴夹角越大,可得直线![]() 与
与![]() 相切时理想值最大,
相切时理想值最大,![]() 与x中相切时,理想值最小,即可得答案;(2)根据题意,讨论
与x中相切时,理想值最小,即可得答案;(2)根据题意,讨论![]() 与
与![]() 轴及直线
轴及直线![]() 相切时,LQ 取最小值和最大值,求出
相切时,LQ 取最小值和最大值,求出![]() 点横坐标即可;(3)根据题意将点
点横坐标即可;(3)根据题意将点![]() 转化为直线
转化为直线![]() ,
,![]() 点理想值最大时点
点理想值最大时点![]() 在
在![]() 上,分析图形即可.
上,分析图形即可.
(1)①∵点![]() 在直线
在直线![]() 上,
上,
∴![]() ,
,
∴点![]() 的“理想值”
的“理想值”![]() =-3,
=-3,
故答案为:﹣3.
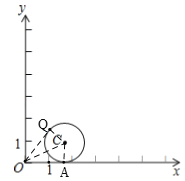
②当点![]() 在
在![]() 与
与![]() 轴切点时,点
轴切点时,点![]() 的“理想值”最小为0.
的“理想值”最小为0.
当点![]() 纵坐标与横坐标比值最大时,
纵坐标与横坐标比值最大时,![]() 的“理想值”最大,此时直线
的“理想值”最大,此时直线![]() 与
与![]() 切于点
切于点![]() ,
,
设点Q(x,y),![]() 与x轴切于A,与OQ切于Q,
与x轴切于A,与OQ切于Q,
∵C(![]() ,1),
,1),
∴tan∠COA=![]() =
=![]() ,
,
∴∠COA=30°,
∵OQ、OA是![]() 的切线,
的切线,
∴∠QOA=2∠COA=60°,
∴![]() =tan∠QOA=tan60°=
=tan∠QOA=tan60°=![]() ,
,
∴点![]() 的“理想值”为
的“理想值”为![]() ,
,
故答案为:![]() .
.
(2)设直线与![]() 轴、
轴、![]() 轴的交点分别为点
轴的交点分别为点![]() ,点
,点![]() ,
,
当x=0时,y=3,
当y=0时,![]() x+3=0,解得:x=
x+3=0,解得:x=![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,
∴tan∠OAB=![]() ,
,
∴![]() .
.
∵![]() ,
,
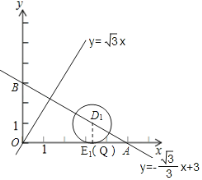
∴①如图,作直线![]() .
.
当![]() 与
与![]() 轴相切时,LQ=0,相应的圆心
轴相切时,LQ=0,相应的圆心![]() 满足题意,其横坐标取到最大值.
满足题意,其横坐标取到最大值.
作![]() 轴于点
轴于点![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() 的半径为1,
的半径为1,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∴![]() .
.
②如图
当![]() 与直线
与直线![]() 相切时,LQ=
相切时,LQ=![]() ,相应的圆心
,相应的圆心![]() 满足题意,其横坐标取到最小值.
满足题意,其横坐标取到最小值.
作![]() 轴于点
轴于点![]() ,则
,则![]() .
.
设直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
∵直线![]() 中,k=
中,k=![]() ,
,
∴![]() ,
,
∴![]() ,点F与Q重合,
,点F与Q重合,
则![]() .
.
∵![]() 的半径为1,
的半径为1,
∴![]() .
.
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∴![]() .
.
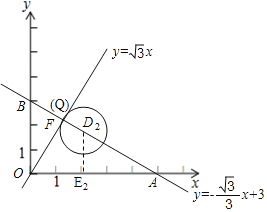
由①②可得,![]() 的取值范围是
的取值范围是![]() .
.
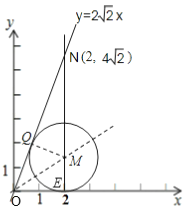
(3)∵M(2,m),
∴M点在直线x=2上,
∵![]() ,
,
∴LQ取最大值时,![]() =
=![]() ,
,
∴作直线y=![]() x,与x=2交于点N,
x,与x=2交于点N,
当![]() M与ON和x轴同时相切时,半径r最大,
M与ON和x轴同时相切时,半径r最大,
根据题意作图如下:![]() M与ON相切于Q,与x轴相切于E,
M与ON相切于Q,与x轴相切于E,
把x=2代入y=![]() x得:y=4
x得:y=4![]() ,
,
∴NE=4![]() ,OE=2,ON=
,OE=2,ON=![]() =6,
=6,
∴∠MQN=∠NEO=90°,
又∵∠ONE=∠MNQ,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:r=![]() .
.
∴最大半径为![]() .
.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y1=x2﹣2x﹣3,一次函数y2=x﹣1.
(1)在同一坐标系中,画出这两个函数的图象;
(2)根据图形,求满足y1>y2的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
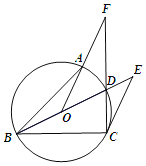
【题目】已知,如图,BD为⊙O的直径,点A、C在⊙O上并位于BD的两侧,∠ABC=45°,连结CD、OA并延长交于点F,过点C作⊙O的切线交BD延长线于点E.
(1)求证:∠F=∠ECF;
(2)当DF=6,tan∠EBC=![]() ,求AF的值.
,求AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学的一个数学兴趣小组在本校学生中开展了主题为“雾霾知多少”的专题调查括动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“A.非常了解”、“B.比较了解”、“C.基本了解”、“D.不太了解”四个等级,将所得数据进行整理后,绘制成如下两幅不完整的统计图表,请你结合图表中的信息解答下列问题
等级 | A | B | C | D |
频数 | 40 | 120 | 36 | n |
频率 | 0.2 | m | 0.18 | 0.02 |
(1)表中m= ,n= ;
(2)扇形统计图中,A部分所对应的扇形的圆心角是 °,所抽取学生对丁雾霾了解程度的众数是 ;
(3)若该校共有学生1500人,请根据调查结果估计这些学生中“比较了解”人数约为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点A(3,m).
交于点A(3,m).
(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于![]() 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数![]() 的图象于点N.
的图象于点N.
①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七、八年级各选派10名选手参加学校举办的环保知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.竞赛后,两支代表队选手的不完整成绩分布如下所示:


(1)通过计算,补全表格;
(2)有人说七年级的合格率、优秀率均高于八年级,所以七年级代表队成绩比八年级代表队好.但也有人说八年级代表队成绩比七年级代表队好.请你给出两条支持八年级代表队成绩较好的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
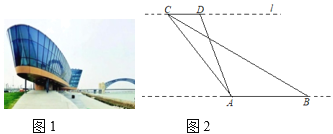
【题目】全国第二届青年运动会是山西省历史上第一次举办的大型综合性运动会,太原作为主赛区,新建了很多场馆,其中在汾河东岸落成了太原水上运动中心,它的终点塔及媒体中心是一个以“大帆船”造型(如图1),外观极具创新,这里主要承办赛艇、皮划艇、龙舟等项目的比赛.“青春”数学兴趣小组为了测量“大帆船”AB的长度,他们站在汾河西岸,在与AB平行的直线l上取了两个点C、D,测得CD=40m,∠CDA=120°,∠ACB=18.5°,∠BCD=26.5°,如图2.请根据测量结果计算“大帆船”AB的长度.(结果精确到0.1m,参考数据:sin26.5°≈0.45,tan26.5°≈0.50,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
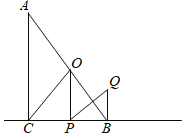
【题目】如图所示,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与B、C重合),连接OC、OP,将OP绕点P顺时针旋转60°,得到线段PQ,连接BQ,若∠BPO=15°,BP=4,则BQ的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
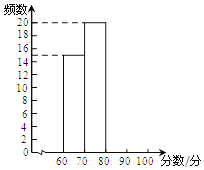
【题目】某学校组织七年级学生进行“垃圾分类”知识测试,现随机抽取部分学生的成绩进行统计,并绘制如下频数分布表以及频数分布直方图.
分数档 | 分数段/分 | 频数 | 频率 |
A | 90<x≤100 | a | 0.12 |
B | 80<x≤90 | b | 0.18 |
C | 70<x≤80 | 20 | c |
D | 60<x≤70 | 15 | d |
请根据以上信息,解答下列问题:
(1)已知A,B档的学生人数之和等于D档学生人数,求被抽取的学生人数,并把频数分布直方图补充完整.
(2)该校七年级共有200名学生参加测试,请估计七年级成绩在C档的学生人数.
(3)你能确定被抽取的这些学生的成绩的众数在哪一档吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com