
����Ŀ��ȫ���ڶ��������˶�����ɽ��ʡ��ʷ�ϵ�һ�ξٰ�Ĵ����ۺ����˶��ᣬ̫ԭ��Ϊ���������½��˺ܶೡ�ݣ������ڷںӶ��������̫ԭˮ���˶����ģ������յ�����ý��������һ���ԡ��������ͣ���ͼ1������ۼ��ߴ��£�������Ҫ�а���ͧ��Ƥ��ͧ�����۵���Ŀ�ı���.���ഺ����ѧ��ȤС��Ϊ�˲���������AB�ij��ȣ�����վ�ڷں�����������ABƽ�е�ֱ��l��ȡ��������C��D�����CD=40m����CDA=120�㣬��ACB=18.5�㣬��BCD=26.5�㣬��ͼ2������ݲ���������㡰����AB�ij��ȣ��������ȷ��0.1m,�ο����ݣ�sin26.5���0.45��tan26.5���0.50��![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��
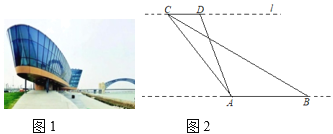
���𰸡�������AB�ij���ԼΪ94.8m
��������
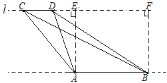
�ֱ����A��B��ֱ��l�Ĵ��ߣ�����ֱ�Ϊ��E��F����DE=xm����BF= AE=CE=( x +40)m��AE=![]() x ���г����̣����x��ֵ������������⣮
x ���г����̣����x��ֵ������������⣮
�ֱ����A��B��ֱ��l�Ĵ��ߣ�����ֱ�Ϊ��E��F��
��DE=xm����֪�ı���ABFE�Ǿ��Σ�
�� AB=EF��AE=BF��
����DCA=��ACB+��BCD=18.5��+26.5��=45�㣬
�� BF= AE=CE=( x +40)m��
�� ��CDA=120����
�� ��ADE=60�㣮
�� AE= x��tan60��=![]() x ��
x ��
�� ![]() x= x +40 �� ��ã� x��54.79��m����
x= x +40 �� ��ã� x��54.79��m����
�� BF= CE =54.79+40=94.79��m����
�� CF=![]() ��189.58��m����
��189.58��m����
�� EF= CF- CE=189.58-94.79��94.8��m����
�� AB=94.8��m����
�𣺡�����AB�ij���ԼΪ94.8m��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У����ǰѺᡢ�����궼�������ĵ�������㣮��֪��A��0��4������B��x���������ϵ����㣬�ǡ�AOB�ڲ����������߽磩���������Ϊm������B�ĺ�����Ϊ4ʱ��m��ֵ��_____������B�ĺ�����Ϊ4n��nΪ��������ʱ��m��_____���ú�n�Ĵ���ʽ��ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijˮ���ӹ���˾�����βɹ���һ�����ӣ���һ�η���Ϊ25��Ԫ���ڶ��η���Ϊ30��Ԫ����֪��һ�βɹ�ʱÿ�����ӵļ۸��ȥ���ƽ���۸�������0.1��Ԫ���ڶ��βɹ�ʱÿ�����ӵļ۸��ȥ���ƽ���۸��½���0.1��Ԫ���ڶ��βɹ��������ǵ�һ�βɹ�������2����
��1������ȥ��ÿ�����ӵ�ƽ���۸��Ƕ�����Ԫ�����βɹ����������Ƕ��ٶ֣�
��2���ù�˾�ɽ����Ӽӹ����Ҹ�����֭��ÿ��ֻ�ܼӹ�����һ�֣��������ӹ����Ҹ���ÿ��ɼӹ�3�����ӣ�ÿ�ֿɻ���0.7��Ԫ���������ӹ�����֭��ÿ��ɼӹ�9�����ӣ�ÿ�ֿɻ���0.2��Ԫ.Ϊ������Ҫ�����вɹ������ӱ�����30���ڼӹ���ϣ�
�ٸ��ݸù�˾�������������ӹ��Ҹ���ʱ�䲻�ܳ��������죿
������μӹ����������У�Ӧ�����ٶ����Ӽӹ����Ҹ����ܻ�ȡ��������������Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵ![]() �еĵ�
�еĵ�![]() ��������������
��������������![]() �������
�������![]() �ı�
�ı�![]() ��Ϊ��
��Ϊ��![]() ��������ֵ��������
��������ֵ��������![]() ����
����![]() ��������ֵ��
��������ֵ��![]() ��
��
��1��������![]() ��ֱ��
��ֱ��![]() �ϣ����
�ϣ����![]() ��������ֵ��
��������ֵ��![]() ����_______��
����_______��
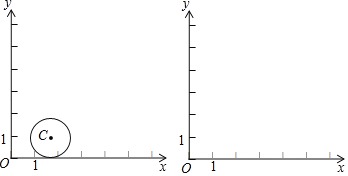
����ͼ��![]() ��
��![]() �İ뾶Ϊ1������
�İ뾶Ϊ1������![]() ��
��![]() �ϣ����
�ϣ����![]() ��������ֵ��
��������ֵ��![]() ��ȡֵ��Χ��_______��
��ȡֵ��Χ��_______��
��2����![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�![]() �İ뾶Ϊ1����
�İ뾶Ϊ1����![]() ��
��![]() ���˶�ʱ����
���˶�ʱ����![]() �����
�����![]() �����
�ĺ�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��![]() ��
��![]() ����
����![]() Ϊ�뾶��
Ϊ�뾶��![]() ������һ�㣬��
������һ�㣬��![]() ʱ�������������������Բ����ֱ��д����Ӧ�İ뾶
ʱ�������������������Բ����ֱ��д����Ӧ�İ뾶![]() ��ֵ����Ҫ��ͼλ��ȷ�������س߹���ͼ��
��ֵ����Ҫ��ͼλ��ȷ�������س߹���ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺��һ���ɱ�Ϊÿ��30Ԫ����Ʒ���̵갴���۲����ڳɱ��ۣ��Ҳ�����50Ԫ���ۣ������鷢�֣�����Ʒÿ���������y�����������۵���x��Ԫ��֮������һ�κ�����ϵ����ͼ����ͼ��ʾ��
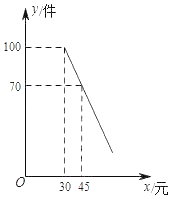
��1�������Ʒÿ���������y�����������۵���x��Ԫ��֮��ĺ�����ϵʽ��
��2�����۵��۶�Ϊ����Ԫʱ������ʹ���۸���Ʒÿ���õ�����w��Ԫ�������������Ƕ��٣�
��3�����̵�Ҫʹ���۸���Ʒÿ���õ��������800Ԫ����ֱ��д��ÿ���������y��������ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
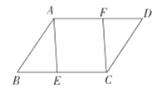
����Ŀ�����꼶6���һ������ѧϰС���鳤�ռ�����������Ա��������������ʱ�������������ͼ��ʾ�����ı���![]() �У���
�У���![]() �ֱ��ڱ�
�ֱ��ڱ�![]() �ϣ�____________________����֤���ı���
�ϣ�____________________����֤���ı���![]() ��ƽ���ı��Σ������ں��������������Ҽ�ݵ�����ʹ���۳����������ֱ���:��
��ƽ���ı��Σ������ں��������������Ҽ�ݵ�����ʹ���۳����������ֱ���:��![]() ����
����![]() ����
����![]() �����ı���
�����ı���![]() ��ƽ���ı��Σ�����A��B��C��D��λͬѧ��������������ĿҪ����ǣ�������
��ƽ���ı��Σ�����A��B��C��D��λͬѧ��������������ĿҪ����ǣ�������
A.�٢�B.�٢ڢ�C.�٢�D.��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������500ǿH��˾��������ij�ݳ�����Ʊ������������Ա�����ݳ���Ĺ�Ʊ��ʽ���������֣�
��ʽһ������λ��������10��Ԫ����õ�λ������Ʊ�ļ۸�Ϊÿ��0.02��Ԫ�������ܷ��ã����������+��Ʊ�ѣ���
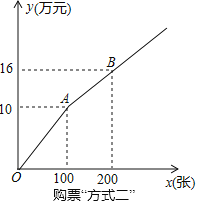
��ʽ������ͼ��ʾ���蹺����Ʊx�ţ��ܷ���Ϊy��Ԫ
��1�����ù�Ʊ����ʽһ��ʱy��x�ĺ�����ϵʽ��
��2����H��A���ҹ�˾�ֱ���÷�ʽһ����ʽ�������ݳ�����Ʊ��400�ţ���A��˾����100�ţ�����˾������27.2��Ԫ����H��A����˾��������Ʊ�����ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��AOB�ǵ���ֱ�������Σ���AOB=90������A��2,1��.
��1�����B�����ꣻ
��2����A��O��B����������ߵĺ�������ʽ��
��3���ڣ�2��������������ϣ��Ƿ����һ��P��ʹ�ı���ABOP�������������ڣ������P�����ꣻ�������ڣ���˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���B������Ϊ��4��2����ֱ��y=��![]() x+
x+![]() ���AB��BC�ֱ��ཻ�ڵ�M��N������y=
���AB��BC�ֱ��ཻ�ڵ�M��N������y=![]() ��x��0����ͼ�����M��
��x��0����ͼ�����M��
��1����˵����NҲ�ں���y=![]() ��x��0����ͼ���ϣ�
��x��0����ͼ���ϣ�
��2����ֱ��MN��y��ĸ�����ƽ�Ƶõ�ֱ��M��N�䣬��ֱ��M��N���뺯��y�T![]() ��x��0����ͼ�����һ������ʱ����ֱ��M'N��Ľ���ʽ��
��x��0����ͼ�����һ������ʱ����ֱ��M'N��Ľ���ʽ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com