
����Ŀ������ijˮ���ӹ���˾�����βɹ���һ�����ӣ���һ�η���Ϊ25��Ԫ���ڶ��η���Ϊ30��Ԫ����֪��һ�βɹ�ʱÿ�����ӵļ۸��ȥ���ƽ���۸�������0.1��Ԫ���ڶ��βɹ�ʱÿ�����ӵļ۸��ȥ���ƽ���۸��½���0.1��Ԫ���ڶ��βɹ��������ǵ�һ�βɹ�������2����
��1������ȥ��ÿ�����ӵ�ƽ���۸��Ƕ�����Ԫ�����βɹ����������Ƕ��ٶ֣�
��2���ù�˾�ɽ����Ӽӹ����Ҹ�����֭��ÿ��ֻ�ܼӹ�����һ�֣��������ӹ����Ҹ���ÿ��ɼӹ�3�����ӣ�ÿ�ֿɻ���0.7��Ԫ���������ӹ�����֭��ÿ��ɼӹ�9�����ӣ�ÿ�ֿɻ���0.2��Ԫ.Ϊ������Ҫ�����вɹ������ӱ�����30���ڼӹ���ϣ�
�ٸ��ݸù�˾�������������ӹ��Ҹ���ʱ�䲻�ܳ��������죿
������μӹ����������У�Ӧ�����ٶ����Ӽӹ����Ҹ����ܻ�ȡ��������������Ϊ���٣�
���𰸡���1��ȥ��ÿ�����ӵ�ƽ���۸���0.4��Ԫ/�֣����βɹ���������Ϊ150�֣���2���ټӹ��Ҹ���ʱ�䲻�ܳ���20�죻��Ӧ��60�����Ӽӹ����Ҹ����ܻ�ȡ��������������Ϊ60��Ԫ��
��������
��1�����ݵڶ��βɹ��������ǵ�һ�βɹ�������2���з��̼������ȥ��ÿ�����ӵ�ƽ���۸�Ȼ���ټ������βɹ�����������
��2���ٸ������вɹ������ӱ�����30���ڼӹ�����г�����ʽ��⼴�ɣ�
����ù�˾�ӹ��Ҹ�![]() �죬����������Ϊ
�죬����������Ϊ![]() ��Ԫ�����������г�
��Ԫ�����������г�![]() ����x�ĺ�������ʽ������һ�κ�����������⼴�ɣ�
����x�ĺ�������ʽ������һ�κ�����������⼴�ɣ�
�⣺��1����ȥ��ÿ�����ӵ�ƽ���۸���![]() ��Ԫ/�֣�
��Ԫ/�֣�
�����⣬�ã�![]() ��
��
��ã�![]() ��
��
�����飬![]() ��ԭ���̵Ľ⣬
��ԭ���̵Ľ⣬
![]() ���֣���
���֣���
��ȥ��ÿ�����ӵ�ƽ���۸���0.4��Ԫ/�֣����βɹ���������Ϊ150�֣�
��2������ù�˾�ӹ��Ҹ���![]() �죬
�죬
��![]() ��
��
��ã�![]() ��
��
���Լӹ��Ҹ���ʱ�䲻�ܳ���20�죻
����ù�˾�ӹ��Ҹ�![]() �죬����������Ϊ
�죬����������Ϊ![]() ��Ԫ��
��Ԫ��
�����⣬��![]() ��
��
��![]() ��
��
��![]() ��
��![]() �����������
�����������
��![]() ��
��
�൱![]() ʱ��
ʱ��![]() ����Ԫ����
����Ԫ����
��![]() ���֣���
���֣���
��Ӧ��60�����Ӽӹ����Ҹ����ܻ�ȡ��������������Ϊ60��Ԫ��


 ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д� ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У���
����![]() ��
��![]() ��
��![]() �����DZ�
�����DZ�![]() ���ĵȷֵ㣬��
���ĵȷֵ㣬��![]() ��
��![]() ��
��![]() �����DZ�
�����DZ�![]() ���ĵȷֵ㣬�ֱ���
���ĵȷֵ㣬�ֱ���![]() ��
��![]() ��
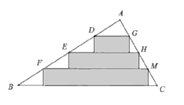
��![]() Ϊ�����¼���������ȵľ��Σ���ͼ��ʾ����ͼ�пհײ��ֵ������Ϊ
Ϊ�����¼���������ȵľ��Σ���ͼ��ʾ����ͼ�пհײ��ֵ������Ϊ![]() ����ͼ����Ӱ���ֵ�������ǣ� ��
����ͼ����Ӱ���ֵ�������ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��ax2+bx+c��a��0����x�ύ�ڵ�A����1��0������y��Ľ����ڣ�0��2������0��3��֮�䣨�����˵㣩����������Ϊ��1��n���������н��ۣ�
��4a+2b��0��
�ک�1��a��![]() ��
��
����������ʵ��m��a+b��am2+bm�ܳ�����
������x�ķ���ax2+bx+c��n��1����������ȵ�ʵ������
���н�����ȷ�ĸ���Ϊ��������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
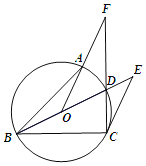
����Ŀ����֪����ͼ��BDΪ��O��ֱ������A��C����O�ϲ�λ��BD�����࣬��ABC��45�㣬����CD��OA���ӳ����ڵ�F������C����O�����߽�BD�ӳ����ڵ�E��
��1����֤����F����ECF��
��2����DF��6��tan��EBC��![]() ����AF��ֵ��
����AF��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ί��������֯һ�Ρ���ѧ֮�á���������ĸ�����ѧ���ط���ѡ����ɽ������ɽ��®ɽ��������о���ɽ������Ǻ�ɫ����ʤ�أ���У��ί����ͨ����ǩ��ʽȷ�����������ط���
��ǩ�����ĸ��ط��ֱ�д��4����ȫ��ͬ��ֽ�����棬��4��ֽ�Ʊ��泯�ϣ�ϴ�Ⱥ���������ϣ���ί���С���ȴ��������ȡһ��ֽ�ƣ����µ������ٴ�ʣ�µ�ֽ���������ȡ�ڶ��ţ����µ�����
��1������˵���У���ȷ�������______��
�ٵ�һ�Ρ����о���ɽ���ĸ�����![]() ��
��
�ڡ����е��������ط��Ǻ�ɫ����ʤ�ء��DZ�Ȼ�¼���
�ۡ����е��������ط��Ǻ�ɫ����ʤ�ء�������¼���
�ܡ����е��������ط��Ǻ�ɫ����ʤ�ء��Dz������¼���
��2������״ͼ�����б�������ʾ���γ������п��ܳ��ֵĽ���������е��������ط��Ǻ�ɫ����ʤ�ء��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��һ����ѧ��ȤС���ڱ�Уѧ���п�չ������Ϊ������֪��������ר�������������ȡ��������ķ�ʽ�����ʾ����飬�ʾ�����Ľ����Ϊ��A���dz��˽�������B���Ƚ��˽�������C�������˽�������D����̫�˽����ĸ��ȼ������������ݽ����������Ƴ�����������������ͳ��ͼ����������ͼ���е���Ϣ�����������
�ȼ� | A | B | C | D |
Ƶ�� | 40 | 120 | 36 | n |
Ƶ�� | 0.2 | m | 0.18 | 0.02 |
��1������m���� ����n���� ����
��2������ͳ��ͼ�У�A��������Ӧ�����ε�Բ�Ľ����� ����������ȡѧ���Զ������˽�̶ȵ��������� ����
��3������У����ѧ��1500�ˣ�����ݵ�����������Щѧ�������Ƚ��˽�������ԼΪ���٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�����
�У�����![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() ���ڵ�A(3,m).
���ڵ�A(3,m).
��1����k��m��ֵ��
��2����֪��P(n��n)(n>0)������P��ƽ����![]() ���ֱ�ߣ���ֱ��y=x-2�ڵ�M������P��ƽ����y���ֱ�ߣ�������
���ֱ�ߣ���ֱ��y=x-2�ڵ�M������P��ƽ����y���ֱ�ߣ�������![]() ��ͼ���ڵ�N.
��ͼ���ڵ�N.
�ٵ�n=1ʱ���ж��߶�PM��PN��������ϵ����˵�����ɣ�
����PN��PM����Ϻ�����ͼ��ֱ��д��n��ȡֵ��Χ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
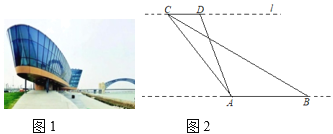
����Ŀ��ȫ���ڶ��������˶�����ɽ��ʡ��ʷ�ϵ�һ�ξٰ�Ĵ����ۺ����˶��ᣬ̫ԭ��Ϊ���������½��˺ܶೡ�ݣ������ڷںӶ��������̫ԭˮ���˶����ģ������յ�����ý��������һ���ԡ��������ͣ���ͼ1������ۼ��ߴ��£�������Ҫ�а���ͧ��Ƥ��ͧ�����۵���Ŀ�ı���.���ഺ����ѧ��ȤС��Ϊ�˲���������AB�ij��ȣ�����վ�ڷں�����������ABƽ�е�ֱ��l��ȡ��������C��D�����CD=40m����CDA=120�㣬��ACB=18.5�㣬��BCD=26.5�㣬��ͼ2������ݲ���������㡰����AB�ij��ȣ��������ȷ��0.1m,�ο����ݣ�sin26.5���0.45��tan26.5���0.50��![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
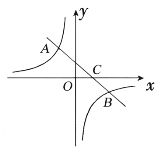
����Ŀ����ͼ��һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ���ڶ����������ڵ�
��ͼ���ڶ����������ڵ�![]() ���㣬��
���㣬��![]() �ύ��
�ύ��![]() �㣬��
�㣬��![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]()
��1����÷�����������һ�κ����Ľ���ʽ��
��2������![]() ��
��![]() ����
����![]() �������
�������
��3�����![]() ��
��![]() ���ϣ�������
���ϣ�������![]() ��ֱ�������Σ�ֱ��д����
��ֱ�������Σ�ֱ��д����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com