
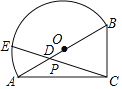
【题目】如图,一块∠BAC为30°的直角三角板ABC的斜边AB与量角器的直径恰好重合,点E在量角器的圆弧边缘处从A到B运动,连接CE,交直径AB于点D.
(1)当点E在量角器上对应的刻度是90°时,则∠ADE的度数为______;
(2)若AB=8,P为CE的中点,当点E从A到B的运动过程中,点P也随着运动,则点P所走过的路线长为______.
【答案】75° 2π
【解析】
(1)连接OE.根据∠ACE=![]() ∠AOE=45°,∠ADE=∠A+∠ACE求解即可;
∠AOE=45°,∠ADE=∠A+∠ACE求解即可;
(2)连接OP,设OC的中点为O′.由PE=PC,推出OP⊥EC,推出∠OPC=90°,推出点P的运动轨迹是以OC为直径的半圆,由此即可解决问题;
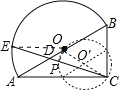
解:(1)如图,连接OE.
∵直角三角板ABC的斜边AB与量角器的直径恰好重合,
∴点A,E,B,C共圆,
∵点E对应的刻度是90°,
∴∠AOE=90°,
∴∠ACE=![]() ∠AOE=45°,
∠AOE=45°,
∴∠ADE=∠A+∠ACE=75°.
故答案为75°.
(2)连接OP,设OC的中点为O′.
∵PE=PC,
∴OP⊥EC,
∴∠OPC=90°,
∴点P的运动轨迹是以OC为直径的半圆,
∵OC=![]() AB=4,
AB=4,
∴OO′=![]() OC=2,
OC=2,
∴点P的运动路径的长为π2=2π,
故答案为2π


科目:初中数学 来源: 题型:
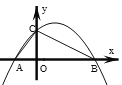
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() ,(
,(![]() 左
左![]() 右),交y轴于点C,△AOC的周长为12,sin∠CBA=
右),交y轴于点C,△AOC的周长为12,sin∠CBA=![]() ,则下列结论:①A点坐标(-3,0);②a=
,则下列结论:①A点坐标(-3,0);②a=![]() ;③点B坐标(8,0);④对称轴x=
;③点B坐标(8,0);④对称轴x=![]() .其中正确的有( )个.
.其中正确的有( )个.
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在北部湾经济区农业示范基地采购A,B两种农产品,已知A种农产品每千克的进价比B种多2元,且用24000元购买A种农产品的数量(按重量计)与用18000元购买B种农产品的数量(按重量计)相同.
(1)求A,B两种农产品每千克的进价分别是多少元?
(2)该公司计划购进A,B两种农产品共40吨,并运往异地销售,运费为500元/吨,已知A种农产品售价为15元/kg,B种农产品售价为12元/kg,其中A种农产品至少购进15吨且不超过B种农产品的数量,问该公司应如何采购才能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用总长10m的铝合金材料做一个如图所示的窗框(不计损耗),窗框的上部是等腰直角三角形,下部是两个全等的矩形,窗框的总面积为3m2(材料的厚度忽略不计).若设等腰直角三角形的斜边长为xm,下列方程符合题意的是( )

A. ![]() B.
B. ![]()
C. ![]() =3D.
=3D. ![]() =3
=3
查看答案和解析>>
科目:初中数学 来源: 题型:
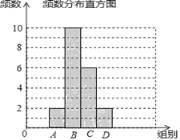
【题目】张老师把微信运动里“好友计步榜”排名前20的好友一天行走的步数做了整理,绘制了如下不完整的统计图表:
组别 | 步数分组 | 频率 |
A | x<6000 | 0.1 |
B | 6000≤x<7000 | 0.5 |
C | 7000≤x<8000 | m |
D | x≥8000 | n |
合计 | 1 |
根据信息解答下列问题:
(1)填空:m= ,n= ;并补全条形统计图;
(2)这20名朋友一天行走步数的中位数落在 组;(填组别)
(3)张老师准备随机给排名前4名的甲、乙、丙、丁中的两位点赞,请求出甲、乙被同时点赞的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过点A(-1,0)、B(3,0)、C(0,3)三点.
(1)求抛物线相应的函数表达式;
(2)点M是线段BC上的点(不与B、C重合),过M作MN∥y轴交抛物线于N,连接NB.若点M的横坐标为t,是否存在t,使MN的长最大?若存在,求出sin∠MBN的值;若不存在,请说明理由;
(3)若对一切x≥0均有ax2+bx+c≤mx-m+13成立,求实数m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
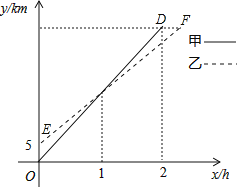
【题目】在一条笔直的公路上依次有A、B、C三地,自行车爱好者甲、乙两人分别从A、B两地同时出发,沿直线匀速骑向C地.已知甲的速度为20km/h,如图所示,甲、乙两人与A地的距离y(km)与行驶时间x(h)的函数图象分别为线段OD、EF.
(1)A、B两地的距离为______km.
(2)求线段EF所在直线对应的函数关系式.
(3)若两人在出发时都配备了通话距离为3km的对讲机,求甲、乙两人均在骑行过程中可以用对讲机通话的时间段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.
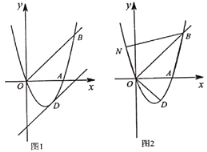
(1)求抛物线的解析式;
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标;
(3)如图,已知点N在抛物线上,且![]() .
.
①求出点N的坐标;
②在(2)的条件下,直接写出所有满足![]() 的点P的坐标.
的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“驴友”小明分三次从M地出发沿着不同的线路![]() 线,B线,C线
线,B线,C线![]() 去N地
去N地![]() 在每条线路上行进的方式都分为穿越丛林、涉水行走和攀登这三种
在每条线路上行进的方式都分为穿越丛林、涉水行走和攀登这三种![]() 他涉水行走4小时的路程与攀登6小时的路程相等
他涉水行走4小时的路程与攀登6小时的路程相等![]() 线、C线路程相等,都比A线路程多
线、C线路程相等,都比A线路程多![]() ,A线总时间等于C线总时间的
,A线总时间等于C线总时间的![]() ,他用了3小时穿越丛林、2小时涉水行走和2小时攀登走完A线,在B线中穿越丛林、涉水行走和攀登所用时间分别比A线上升了
,他用了3小时穿越丛林、2小时涉水行走和2小时攀登走完A线,在B线中穿越丛林、涉水行走和攀登所用时间分别比A线上升了![]() ,
,![]() ,
,![]() ,若他用了x小时穿越丛林、y小时涉水行走和z小时攀登走完C线,且x,y,z都为正整数,则
,若他用了x小时穿越丛林、y小时涉水行走和z小时攀登走完C线,且x,y,z都为正整数,则![]() ______.
______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com