
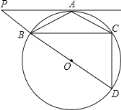
【题目】已知:如图,![]() 是
是![]() 的外接圆,且
的外接圆,且![]() ,
,![]() ,
,![]() 是
是![]() 的切线,
的切线,![]() 为切点,割线
为切点,割线![]() 过圆心,交
过圆心,交![]() 于另一点
于另一点![]() ,连接
,连接![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 求
求![]() 的半径及
的半径及![]() 的长.
的长.
【答案】(1)证明见解析;(2) DC=23.8.
【解析】
(1)如图;由AB=AC,可以得到∠1=∠2,然后利用弦切角定理就可以证得PA与BC的内错角相等,由此得证;
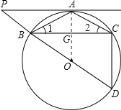
(2)本题需构建直角三角形求解,连接OA,交BC于G,由垂径定理知:OA垂直平分BC,
在Rt△ABG中,已知了AB、BG的长,根据勾股定理可求出AG的长,
在Rt△OBG中,用圆的半径表示出OG的长,然后根据勾股定理,求出圆的半径长,进而可求出OG的长,
△BCD中,易证得OG是△BCD的中位线,由此可求出CD的长.
解:![]() ∵
∵![]() 是
是![]() 的切线,
的切线,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
![]() 连接
连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() ;
;
由![]() 可知,
可知,![]() ,
,
∴![]() .
.
∴![]() 为
为![]() 的中点,
的中点,
∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
设![]() 的半径为
的半径为![]() ,则
,则![]() ,
,
在![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ;
;
∵![]() 是
是![]() 的直径,
的直径,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∵点![]() 是
是![]() 的中点,
的中点,
∴![]() .
.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:在![]() 中,
中,![]() .
.
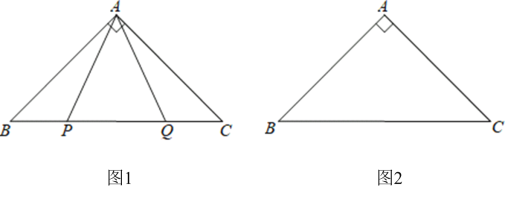
(1)如图1,![]() 是
是![]() 边上两点,
边上两点,![]() , 求
, 求![]() 的度数.
的度数.
(2)点![]() 是
是![]() 边上两动点(不与
边上两动点(不与![]() 重合), 点
重合), 点![]() 在点
在点![]() 左侧,且
左侧,且![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() .
.
①依题意将图2补全.
②小明通过观察和实验,提出猜想:在点![]() 运动的过程中,始终有
运动的过程中,始终有![]() 为等腰直角三角形,他把这个猜想与同学们进行交流,通过讨论,形成以下证明猜想的思路:要想证明
为等腰直角三角形,他把这个猜想与同学们进行交流,通过讨论,形成以下证明猜想的思路:要想证明![]() 为等腰直角三角形,只需证
为等腰直角三角形,只需证![]() .
.
请参考上面的思路,帮助小明证明△APM 为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
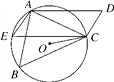
【题目】如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.
(1)求证:四边形AECD为平行四边形;
(2)连接CO,求证:CO平分∠BCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
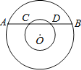
【题目】如图,两同心圆中,大圆的弦![]() 交小圆于
交小圆于![]() 、
、![]() 两点,点
两点,点![]() 到
到![]() 的距离等于
的距离等于![]() 的一半,且
的一半,且![]() .则大小圆的半径之比为( )
.则大小圆的半径之比为( )
A. ![]() :1 B. 2:
:1 B. 2:![]() C. 10:
C. 10:![]() D. 3:1
D. 3:1
查看答案和解析>>
科目:初中数学 来源: 题型:
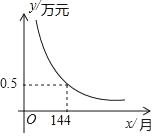
【题目】为了方便孩子入学,小王家购买了一套学区房,交首付款15万元,剩余部分向银行贷款,贷款及贷款利息按月分期还款,每月还款数相同.计划每月还款y万元,x个月还清贷款,若y是x的反比例函数,其图象如图所示:
(1)求y与x的函数解析式;
(2)若小王家计划180个月(15年)还清贷款,则每月应还款多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
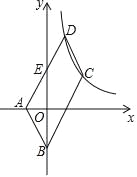
【题目】如图,平行四边形ABCD中,A(-1,0)、B(0,-2),顶点C、D在双曲线![]() (x>0)上,边AD交y轴于点E,若点E恰好是AD的中点,则k=_____.
(x>0)上,边AD交y轴于点E,若点E恰好是AD的中点,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C处测得教学楼顶部D处的仰角为18°,教学楼底部B处的俯角为20°,教学楼的高BD=21m,求实验楼与教学楼之间的距离AB(结果保留整数).(参考数据:tan18°≈0.32,tan20°≈0.36)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com