
����Ŀ����ͼ�٣������κ���y= ![]() x2+bx+c��ͼ����x�ύ��A����2��0����B��3��0�����㣬��A��������������y=
x2+bx+c��ͼ����x�ύ��A����2��0����B��3��0�����㣬��A��������������y= ![]() x��ͼ��ĶԳƵ�ΪC��
x��ͼ��ĶԳƵ�ΪC��
��1����b��c��ֵ��
��2��֤������C������Ķ��κ�����ͼ���ϣ�
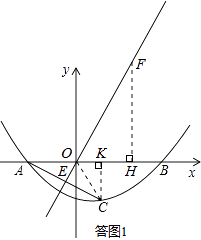
��3����ͼ�ڣ�����B��DB��x�ύ����������y= ![]() x��ͼ���ڵ�D������AC��������������y=
x��ͼ���ڵ�D������AC��������������y= ![]() x��ͼ���ڵ�E������AD��CD���������P�ӵ�A���߶�AD������ÿ��2����λ���ٶ����D�˶���ͬʱ����Q�ӵ�D���߶�DC������ÿ��1����λ���ٶ����C�˶���������һ���㵽���յ�ʱ����һ������ֹ֮ͣ�˶�������PQ��QE��PE�����˶�ʱ��Ϊt�룬�Ƿ����ijһʱ�̣�ʹPEƽ�֡�APQ��ͬʱQEƽ�֡�PQC�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
x��ͼ���ڵ�E������AD��CD���������P�ӵ�A���߶�AD������ÿ��2����λ���ٶ����D�˶���ͬʱ����Q�ӵ�D���߶�DC������ÿ��1����λ���ٶ����C�˶���������һ���㵽���յ�ʱ����һ������ֹ֮ͣ�˶�������PQ��QE��PE�����˶�ʱ��Ϊt�룬�Ƿ����ijһʱ�̣�ʹPEƽ�֡�APQ��ͬʱQEƽ�֡�PQC�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺�ߵ�A����2��0����B��3��0����������y= ![]() x2+bx+c�ϣ�
x2+bx+c�ϣ�
�� 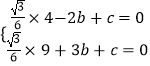 ��
��
��ã�b=�� ![]() ��c=��
��c=�� ![]()
��2��
�⣺���F��ֱ��y= ![]() x�ϣ���F��2��
x�ϣ���F��2�� ![]() ����
����
���ͼ1��ʾ������F��FH��x���ڵ�H����FH= ![]() ��OH=2��
��OH=2��
��tan��FOB= ![]() =
= ![]() �����FOB=60�㣮
�����FOB=60�㣮
���AOE=��FOB=60�㣮
����OC������C��CK��x���ڵ�K��
�ߵ�A��C����y= ![]() x�Գƣ���OC=OA=2����COE=��AOE=60�㣮
x�Գƣ���OC=OA=2����COE=��AOE=60�㣮
���COK=180�㩁��AOE����COE=60�㣮
��Rt��COK��CK=OCsin60��=2�� ![]() =
= ![]() ��OK=OCcos60��=2��
��OK=OCcos60��=2�� ![]() =1��
=1��
��C��1���� ![]() ����
����
�����ߵĽ���ʽΪ��y= ![]() x2��
x2�� ![]() x��
x�� ![]() ����x=1ʱ��y=��
����x=1ʱ��y=�� ![]() ��
��
���C��������κ�����ͼ����
��3��
�⣺������ڣ�
���ͼ1��ʾ����Rt��ACK�У��ɹ��ɶ����ã�AC= ![]() =
= ![]() =
= ![]() ��
��
���ͼ2��ʾ����OB=3����BD=3 ![]() ��AB=OA+OB=5��
��AB=OA+OB=5��
��Rt��ABD�У��ɹ��ɶ����ã�AD= ![]() =
= ![]() =2
=2 ![]() ��
��
�ߵ�A��C����y= ![]() x�Գƣ�
x�Գƣ�
��CD=AD=2 ![]() ����DAC=��DCA��AE=CE=
����DAC=��DCA��AE=CE= ![]() AC=
AC= ![]() ��
��
����PQ��PE��QE�����APE=��QPE����PQE=��CQE��
���ı���APQC�У���DAC+��APQ+��PQC+��DCA=360�㣨�ı����ڽǺ͵���360�㣩��
��2��DAC+2��APE+2��CQE=360�㣬
���DAC+��APE+��CQE=180�㣮
�֡ߡ�DAC+��APE+��AEP=180�㣨�������ڽǺͶ�������
���AEP=��CQE��
�ڡ�APE���CEQ�У��ߡ�DAC=��DCA����AEP=��CQE��
���APE�ס�CEQ��
�� ![]() ������
������ ![]() ��
��
�����ã�2t2�� ![]() t+3=0��
t+3=0��
��ã�t= ![]() ��t=
��t= ![]() ��t��
��t�� ![]() ��������ȥ��
��������ȥ��
�����ijһʱ�̣�ʹPEƽ�֡�APQ��ͬʱQEƽ�֡�PQC����ʱt= ![]()
����������1�����ô���ϵ�������b��c��ֵ����2�����ͼ1��ʾ���ؼ��������C�����꣮�������ֱ��y= ![]() x��x���������Ϊ60�㣬����Ƴ���Rt��COK�У���COK=60�㣬���ֱ�������μ��������C�����ꣻ��3�����ͼ2��ʾ���ؼ���֤����APE�ס�CEQ�����ݡ�DAC=��DCA����AEP=��CQE��֤����APE�ס�CEQ�����������߶α�����ϵ�г����̣��ⷽ�����ʱ��t��ֵ��
x��x���������Ϊ60�㣬����Ƴ���Rt��COK�У���COK=60�㣬���ֱ�������μ��������C�����ꣻ��3�����ͼ2��ʾ���ؼ���֤����APE�ס�CEQ�����ݡ�DAC=��DCA����AEP=��CQE��֤����APE�ס�CEQ�����������߶α�����ϵ�г����̣��ⷽ�����ʱ��t��ֵ��
�����㾫����������Ҫ�����˶��κ�����ͼ��Ͷ��κ��������ʵ����֪ʶ�㣬��Ҫ���ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����ABCD�У�AB��CD��AD��BC�� AB��3��BC��4��������ֽƬ��BD�۵���ʹ��A���ڵ�E������DE��BC�ཻ�ڵ�F.
(1)�жϡ�BDF����״����˵�����ɣ�
(2)��DF�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ���
��ͼ1����ƽ��ֱ������ϵxOy�У���֪��A��a��0����a��0����B��2��3����C��0��3������ԭ��O��ֱ��l��ʹ��������һ�������ޣ�ֱ��l��y������������ɽ���Ϊ�ȣ����ı���OABC��ֱ�ǡ�OCB��ֱ��l�۵�����C���ڵ�D�������ǰ�����������̼�ΪFZ[�ȣ�a]��
��1�������⡿
����D���A�غϣ��������������ΪFZ[ �� ]��
��2�������ԡ�
����DǡΪAB���е㣨��ͼ2������ȣ�
��3������FZ[45�㣬a]��������B���ڵ�E��������E���ı���0ABC�ı�AB�ϣ����a��ֵ������E�����ı���0ABC���ⲿ��ֱ��д��a��ȡֵ��Χ��
��4����̽����
����FZ[�ȣ�a]��������ֱ��CD��x���ڵ�G����ֱ��AB�ڵ�H��ʹ�á�ODG���GAH��һ�����Ƶĵ��������Σ�ֱ��д��FZ[�ȣ�a]��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
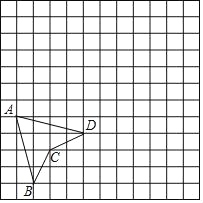
����Ŀ����ͼ������ֽ��ÿ��С�����εı߳�Ϊ1���ı���ABCD�Ķ��㶼�ڸ���ϣ�
(1)�ڷ���ֽ�Ͻ���ƽ��ֱ������ϵ��ʹ�ı���ABCD�Ķ���A��C������ֱ�Ϊ(��5����1)��(��3����3)����д����D�����ꣻ
(2)��(1)����������ϵ�У������ı���ABCD����x��ĶԳ�ͼ��A1B1C1D1����д����B�Ķ�Ӧ��B1�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�EΪBC���ϵ�һ�㣬����AE��BD��AE=AB�� 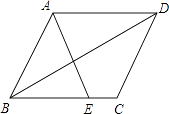
��1����֤����ABE=��EAD��
��2������AEB=2��ADB����֤���ı���ABCD�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2012���ҹ�������������ƽ�ȣ�ȫ��ȫ��������������117210��Ԫ��2008��2012��ȫ�������������뼰�������ٶ������ͼ��ʾ�� 
��1����������ȫ�������������������ٶ���ߵ�������ꣻ
��2��2012���ȫ���������������2011�����Ԫ��
��3���������ȫ�������������������ٶȵ�ƽ������ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y= ![]() x2+bx��
x2+bx�� ![]() ��ͼ����x�ύ�ڵ�A����3��0���͵�B����ABΪ����x���Ϸ���������ABCD����P��x����һ���㣬����DP������P��DP�Ĵ�����y�ύ�ڵ�E��
��ͼ����x�ύ�ڵ�A����3��0���͵�B����ABΪ����x���Ϸ���������ABCD����P��x����һ���㣬����DP������P��DP�Ĵ�����y�ύ�ڵ�E��
��1����ֱ��д����D�����꣺��
��2������P���߶�AO����P����A��O�غϣ����˶����δ�ʱ���߶�OE�ij������ֵ�����������ֵ��
��3���Ƿ���������ĵ�P��ʹ��PED�ǵ��������Σ������ڣ��������P�����꼰��ʱ��PED��������ABCD�ص����ֵ�������������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��D���A��8��0����B��0��6����C��a����a����һƽ���ı��ε��ĸ����㣬��CD������СֵΪ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AD��BC��D �� �����������١�B+��DAC=90�㣻�ڡ�B=��DAC���� ![]() =
= ![]() ����AB2=BDBC �� ����һ���ܹ��ж���ABC��ֱ�������ε��У�������
����AB2=BDBC �� ����һ���ܹ��ж���ABC��ֱ�������ε��У������� 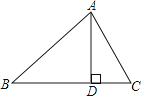
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com