
【题目】已知点D与点A(8,0),B(0,6),C(a,﹣a)是一平行四边形的四个顶点,则CD长的最小值为.
【答案】7 ![]()
【解析】解:有两种情况: ①CD是平行四边形的一条边,那么有AB=CD= ![]() =10
=10
②CD是平行四边形的一条对角线,
过C作CM⊥AO于M,过D作DF⊥AO于F,交AC于Q,过B作BN⊥DF于N,
则∠BND=∠DFA═∠CMA=∠QFA=90°,
∠CAM+∠FQA=90°,∠BDN+∠DBN=90°,
∵四边形ACBD是平行四边形,
∴BD=AC,∠C=∠D,BD∥AC,
∴∠BDF=∠FQA,
∴∠DBN=∠CAM,
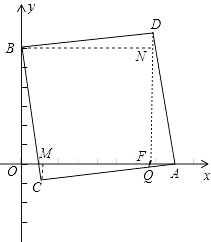
∵在△DBN和△CAM中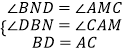
∴△DBN≌△CAM(AAS),
∴DN=CM=a,BN=AM=8﹣a,
D((8﹣a,6+a),
由勾股定理得:CD2=(8﹣a﹣a)2+(6+a+a)2=8a2﹣8a+100=8(a﹣ ![]() )2+98,
)2+98,
当a= ![]() 时,CD有最小值,是
时,CD有最小值,是 ![]()
∵ ![]() <10,
<10,
∴CD的最小值是 ![]() =7
=7 ![]() .
.
解法二:
CD是平行四边形的一条对角线
设CD、AB交于点E,
∵点E为AB的中点,
∴E( ![]() ),即E(4,3)
),即E(4,3)
∵CE=DE,
∴当DE取得最小值时,CE自然为最小,
∵C(a,﹣a),
∴C点可以看成在直线y=﹣x上的一点,
∴CE最小值为点E到直线的距离,即CE⊥直线y=﹣x,
根据两直线垂直,斜率乘积为﹣1,
∴CE所在直线为y=x+b,代入E(4,3),可得y=x﹣1,
∴C点坐标为两直线交点: ![]() ,即:(
,即:( ![]() ,﹣
,﹣ ![]() )
)
∴CE为: ![]() =
= ![]()
∴CD=7 ![]() .
.
所以答案是:7 ![]() .
.
【考点精析】利用平行四边形的性质对题目进行判断即可得到答案,需要熟知平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠A = 3∠C = 90,AB = 3,点Q在边AB上且BQ =![]() ,过Q作QF∥BC交AC于点F,点P在线段QF上,过P作PD∥AC交AB于点D,PE∥AB交BC于点E,当P到△ABC的三边的距离之和为3时,PD + PE + PF =_________.
,过Q作QF∥BC交AC于点F,点P在线段QF上,过P作PD∥AC交AB于点D,PE∥AB交BC于点E,当P到△ABC的三边的距离之和为3时,PD + PE + PF =_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,若二次函数y= ![]() x2+bx+c的图象与x轴交于A(﹣2,0),B(3,0)两点,点A关于正比例函数y=
x2+bx+c的图象与x轴交于A(﹣2,0),B(3,0)两点,点A关于正比例函数y= ![]() x的图象的对称点为C.
x的图象的对称点为C.
(1)求b、c的值;
(2)证明:点C在所求的二次函数的图象上;
(3)如图②,过点B作DB⊥x轴交正比例函数y= ![]() x的图象于点D,连结AC,交正比例函数y=
x的图象于点D,连结AC,交正比例函数y= ![]() x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由.
x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区为方便游客参观,在每个景点均设置两条通道,即楼梯和无障碍通道.如图,已知在某景点P处,供游客上下的楼梯倾斜角为30°(即∠PBA=30°),长度为4m(即PB=4m),无障碍通道PA的倾斜角为15°(即∠PAB=15°).求无障碍通道的长度.(结果精确到0.1m,参考数据:sin15°≈0.21,cos15°≈0.98)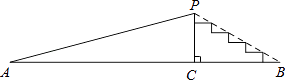
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=ax2+bx﹣3(a,b是常数)的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.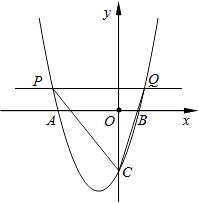
(1)求a和b的值;
(2)求t的取值范围;
(3)若∠PCQ=90°,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”,“科技制作”,“数学思维”,“阅读写作”这四个选修项目的学生(每人限报一课)进行抽样调查,下面是根据收集的数据绘制的不完整的统计图: 
请根据图中提供的信息,解答下面的问题:
(1)此次共调查了名学生,扇形统计图中“艺术鉴赏”部分的圆心角是度;
(2)请把这个条形统计图补充完整;
(3)现该校共有800名学生报名参加这四个选修项目,请你估计其中有多少名学生选修“科技制作”项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一路灯距地面5.6米,身高1.6米的小方从距离灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增长3米,则小方行走的路程AC= . 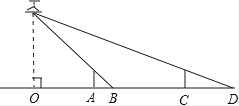
查看答案和解析>>
科目:初中数学 来源: 题型:
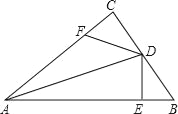
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)请你判断AE、AF与BE之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com