
【题目】Rt△ABC中,∠A = 3∠C = 90,AB = 3,点Q在边AB上且BQ =![]() ,过Q作QF∥BC交AC于点F,点P在线段QF上,过P作PD∥AC交AB于点D,PE∥AB交BC于点E,当P到△ABC的三边的距离之和为3时,PD + PE + PF =_________.
,过Q作QF∥BC交AC于点F,点P在线段QF上,过P作PD∥AC交AB于点D,PE∥AB交BC于点E,当P到△ABC的三边的距离之和为3时,PD + PE + PF =_________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某班10名学生的校服尺寸与对应人数如表所示:
尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
学生人数(人) | 1 | 3 | 2 | 2 | 2 |
则这10名学生校服尺寸的众数和中位数分别为( )
A.165cm,165cm
B.165cm,170cm
C.170cm,165cm
D.170cm,170cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB∥CD,AD∥BC, AB=3,BC=4,将矩形纸片沿BD折叠,使点A落在点E处,设DE与BC相交于点F.
(1)判断△BDF的形状,并说明理由;
(2)求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=![]() ,则△CEF的周长为( )
,则△CEF的周长为( )
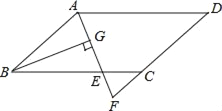
A. 8 B. 9.5 C. 10 D. 11.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C是反比例函数y= ![]() (k<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )
(k<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )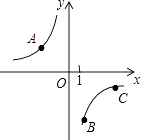
A.4条
B.3条
C.2条
D.1条
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在教学楼上的窗口A看地面上的B、C两个花坛,测得俯角∠EAB=30°,俯角∠EAC=45°.已知教学楼基点D与点C、B在同一条直线上,且B、C两花坛之间的距离为6m.求窗口A到地面的高度AD.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【阅读】
如图1,在平面直角坐标系xOy中,已知点A(a,0)(a>0),B(2,3),C(0,3).过原点O作直线l,使它经过第一、三象限,直线l与y轴的正半轴所成角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
(1)【理解】
若点D与点A重合,则这个操作过程为FZ[ , ];
(2)【尝试】
若点D恰为AB的中点(如图2),求θ;
(3)经过FZ[45°,a]操作,点B落在点E处,若点E在四边形0ABC的边AB上,求出a的值;若点E落在四边形0ABC的外部,直接写出a的取值范围;
(4)【探究】
经过FZ[θ,a]操作后,作直线CD交x轴于点G,交直线AB于点H,使得△ODG与△GAH是一对相似的等腰三角形,直接写出FZ[θ,a].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长为1,四边形ABCD的顶点都在格点上.
(1)在方格纸上建立平面直角坐标系,使四边形ABCD的顶点A,C的坐标分别为(﹣5,﹣1),(﹣3,﹣3),并写出点D的坐标;
(2)在(1)中所建坐标系中,画出四边形ABCD关于x轴的对称图形A1B1C1D1,并写出点B的对应点B1的坐标.
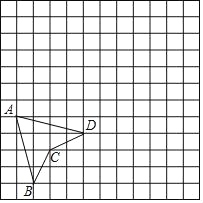
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com