
【题目】如图,二次函数y= ![]() x2+bx﹣
x2+bx﹣ ![]() 的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
(1)请直接写出点D的坐标:;
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;
(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
【答案】
(1)(﹣3,4)
(2)
解:设PA=t,OE=l
由∠DAP=∠POE=∠DPE=90°得△DAP∽△POE
∴ ![]()
∴l=﹣ ![]() +
+ ![]() =﹣
=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]()
∴当t= ![]() 时,l有最大值
时,l有最大值 ![]()
即P为AO中点时,OE的最大值为 ![]()
(3)
解:存在.
①点P点在y轴左侧时,DE交AB于点G,
P点的坐标为(﹣4,0),
∴PA=OP﹣AO=4﹣3=1,
由△PAD≌△EOP得OE=PA=1
∵△ADG∽△OEG
∴AG:GO=AD:OE=4:1
∴AG= ![]() =
= ![]()
∴重叠部分的面积= ![]() =
= ![]()
②当P点在y轴右侧时,P点的坐标为(4,0),
此时重叠部分的面积为 ![]()
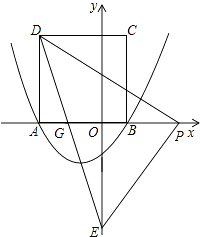
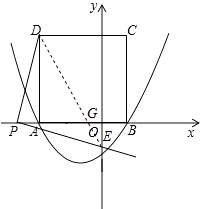
【解析】(1)将点A的坐标代入二次函数的解析式求得其解析式,然后求得点B的坐标即可求得正方形ABCD的边长,从而求得点D的纵坐标;(2)PA=t,OE=l,利用△DAP∽△POE得到比例式,从而得到有关两个变量的二次函数,求最值即可;(3)分点P位于y轴左侧和右侧两种情况讨论即可得到重叠部分的面积.


科目:初中数学 来源: 题型:
【题目】下列这些复杂的图案都是在一个图案的基础上,在“几何画板”软件中拖动一点后形成的,它们中每一个图案都可以由一个“基本图案”通过连续旋转得来,旋转的角度是( )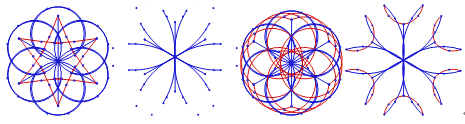
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE. 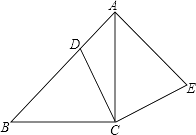
(1)求证:AB⊥AE;
(2)若BC2=ADAB,求证:四边形ADCE为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,若二次函数y= ![]() x2+bx+c的图象与x轴交于A(﹣2,0),B(3,0)两点,点A关于正比例函数y=
x2+bx+c的图象与x轴交于A(﹣2,0),B(3,0)两点,点A关于正比例函数y= ![]() x的图象的对称点为C.
x的图象的对称点为C.
(1)求b、c的值;
(2)证明:点C在所求的二次函数的图象上;
(3)如图②,过点B作DB⊥x轴交正比例函数y= ![]() x的图象于点D,连结AC,交正比例函数y=
x的图象于点D,连结AC,交正比例函数y= ![]() x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由.
x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于点E,BF平分∠ABC,交CD于点F. 
(1)求证:DE=BF;
(2)连接EF,写出图中所有的全等三角形.(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区为方便游客参观,在每个景点均设置两条通道,即楼梯和无障碍通道.如图,已知在某景点P处,供游客上下的楼梯倾斜角为30°(即∠PBA=30°),长度为4m(即PB=4m),无障碍通道PA的倾斜角为15°(即∠PAB=15°).求无障碍通道的长度.(结果精确到0.1m,参考数据:sin15°≈0.21,cos15°≈0.98)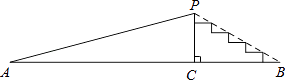
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=ax2+bx﹣3(a,b是常数)的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.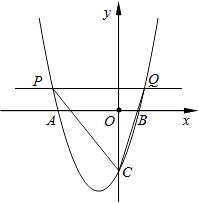
(1)求a和b的值;
(2)求t的取值范围;
(3)若∠PCQ=90°,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AB∥DC , ∠B=90°,E为BC上一点,且AE⊥ED . 若BC=12,DC=7,BE:EC=1:2,
(1)求AB的长.
(2)求△AED的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com