
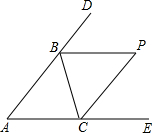
 如图,△ABC的∠ABC、∠ACB的外角的平分线交于点P.
如图,△ABC的∠ABC、∠ACB的外角的平分线交于点P.分析 (1)首先根据三角形的外角的性质,求出∠CBD、∠BCE的度数和是多少;然后根据BP、CP分别是∠CBD、∠BCE的平分线,求出∠CBP、∠BCP的度数和是多少;最后根据三角形的内角和定理,求出∠P的度数是多少即可.
(2)首先根据三角形的外角的性质,求出∠CBD、∠BCE的度数和是多少;然后根据BP、CP分别是∠CBD、∠BCE的平分线,求出∠CBP、∠BCP的度数和是多少;最后根据三角形的内角和定理,求出∠P的度数是多少即可.
(3)首先根据三角形的外角的性质,求出∠CBD、∠BCE的度数和是多少;然后根据BP、CP分别是∠CBD、∠BCE的平分线,求出∠CBP、∠BCP的度数和是多少;最后根据三角形的内角和定理,判断出∠P与∠A的数量关系即可.
解答 解:(1)∵∠CBD=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠CBD+∠BCE=∠A+∠ACB+∠A+∠ACB=180°+∠A=180°+70°=250°,
∵BP、CP分别是∠CBD、∠BCE的平分线,
∴∠CBP=$\frac{1}{2}$∠CBD,∠BCP=$\frac{1}{2}$∠BCE,
∴∠CBP+∠BCP=(∠CBD+∠BCE)÷2=250°÷2=125°,
∴∠P=180°-125°=55°,
即∠P的度数是55°.
(2)∵∠CBD=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠CBD+∠BCE=∠A+∠ACB+∠A+∠ACB=180°+∠A=180°+68°=248°,
∵BP、CP分别是∠CBD、∠BCE的平分线,
∴∠CBP=$\frac{1}{2}$∠CBD,∠BCP=$\frac{1}{2}$∠BCE,
∴∠CBP+∠BCP=(∠CBD+∠BCE)÷2=248°÷2=124°,
∴∠P=180°-124°=56°,
即∠P的度数是56°
(3)∵∠CBD=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠CBD+∠BCE=∠A+∠ACB+∠A+∠ACB=180°+∠A,
∵BP、CP分别是∠CBD、∠BCE的平分线,
∴∠CBP=$\frac{1}{2}$∠CBD,∠BCP=$\frac{1}{2}$∠BCE,
∴∠CBP+∠BCP=(∠CBD+∠BCE)÷2=(180°+∠A)÷2=90°+$\frac{1}{2}$∠A,
∴∠P=180°-(90°+$\frac{1}{2}$∠A)=90°-$\frac{1}{2}$∠A,
即∠P与∠A的数量关系为:∠P=90°-$\frac{1}{2}$∠A.
点评 (1)此题主要考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.
(2)此题还考查了三角形的外角的性质和应用,要熟练掌握,解答此题的关键是要明确:①三角形的外角和为360°.②三角形的一个外角等于和它不相邻的两个内角的和.③三角形的一个外角大于和它不相邻的任何一个内角.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
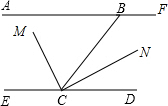 如图:AF∥DE,B为AF上的一点,∠ABC=60°交ED于C,CM平分∠BCE,∠MCN=90°,
如图:AF∥DE,B为AF上的一点,∠ABC=60°交ED于C,CM平分∠BCE,∠MCN=90°,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 140° | B. | 160° | C. | 100° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com