
分析 把方程组的解代入可分别求得a、b的值,可求得答案.
解答 解:
∵方程组$\left\{\begin{array}{l}{2x+y=b}\\{x-by=a}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$,
∴把$\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$代入方程组可得$\left\{\begin{array}{l}{2+6=b}\\{1-6b=a}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-47}\\{b=8}\end{array}\right.$,
∴|a-b|=|-47-8|=|-55|=55,
故答案为:55.
点评 本题主要考查方程组解的定义,根据方程组解的定义求得a、b的值是解题的关键.


科目:初中数学 来源: 题型:解答题
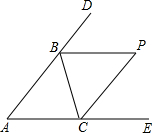 如图,△ABC的∠ABC、∠ACB的外角的平分线交于点P.
如图,△ABC的∠ABC、∠ACB的外角的平分线交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{-7}$ | B. | $\root{3}{2}$ | C. | $\sqrt{{x}^{2}+1}$ | D. | $\root{3}{\frac{b}{a}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知某实验中学有一块四边形的空地ABCD,如下图所示,学校计划在空地上种植草皮,经测量∠A=90°,AC=3m,BD=12m,CB=13m,DA=4m,若每平方米草皮需要300元,问学校需要投入多少资金买草皮?
已知某实验中学有一块四边形的空地ABCD,如下图所示,学校计划在空地上种植草皮,经测量∠A=90°,AC=3m,BD=12m,CB=13m,DA=4m,若每平方米草皮需要300元,问学校需要投入多少资金买草皮?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com