在“平行四边形.矩形.等腰三角形.菱形.正方形这五种图形中.既是轴对称图形.又是中心对称图形的个数为( )A．2B．3C．4D．5 题目和参考答案——青夏教育精英家教网—

8．在“平行四边形、矩形、等腰三角形、菱形、正方形”这五种图形中，既是轴对称图形，又是中心对称图形的个数为（　　）

A．

B．

C．

D．

分析根据轴对称图形与中心对称图形的概念求解．如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．如果一个图形绕某一点旋转180°后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．

解答解：①平行四边形不是轴对称图形，是中心对称图形，不符合题意；
②矩形是轴对称图形，也是中心对称图形，符合题意；
③等腰三角形是轴对称图形，不是中心对称图形，不符合题意；
④菱形是轴对称图形，也是中心对称图形，符合题意；
⑤正方形是轴对称图形，也是中心对称图形，符合题意；
故选B．

点评本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．

练习册系列答案

学府图书寒假作业系列答案

学段衔接提升方案赢在高考寒假作业系列答案

新校园快乐假期系列寒假生活指导系列答案

新思维寒假作业系列答案

新路学业寒假作业快乐假期新疆青少年出版社系列答案

新课堂假期生活假期作业寒假合编系列答案

新课程寒假作业广西师范大学出版社系列答案

新课程寒假作业本系列答案

新课标快乐提优寒假作业陕西旅游出版社系列答案

新课标寒假衔接系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

17．已知抛物线y=x²-2x-3．
（1）求抛物线与x轴的交点坐标；
（2）利用图象说明，当x为何值时，y＞0？y=0？y＜0？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

19．

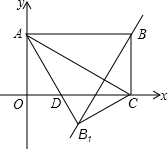如图，矩形OABC在平面直角坐标系中，并且OA、OC的长满足：|OA-2$\sqrt{3}$|+（OC-6）²=0．
（1）求A、B、C三点的坐标．
（2）把△ABC沿AC对折，点B落在点B₁处，AB₁与x轴交于点D，求直线BB₁的解析式．
（3）在直线AC上是否存在点P使PB₁+PD的值最小？若存在，请找出点P的位置，并求出PB₁+PD的最小值；若不存在，请说明理由．
（4）在直线AC上是否存在点P使|PD-PB|的值最大？若存在，请找出点P的位置，并求出|PD-PB|最大值．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

16．若方程组$\left\{\begin{array}{l}{2x+y=b}\\{x-by=a}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$，那么|a-b|=55．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．（1）$\left\{\begin{array}{l}{3x+5y=8}\\{2x-y=1}\end{array}\right.$
（2）$\left\{\begin{array}{l}{\frac{1-2x}{3}-\frac{4-3x}{6}≥\frac{x-2}{2}}\\{2x-7≤3（x-1）}\end{array}\right.$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．计算：4$\sqrt{\frac{1}{2}}$-$\sqrt{18}$+$\sqrt{8}$．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

20．已知关于x的方程$\frac{2x+m}{x-2}$=3的解是正数，那么m的取值范围为（　　）

A．

m＞-6且m≠-2

B．

m＜6

C．

m＞-6且m≠-4