
【题目】(本题6分)下列是用火柴棒拼出的一列图形.

仔细观察,找出规律,解答下列各题:
(1)第4个图中共有_____ 根火柴,第6个图中共有_____ 根火柴;
(2)第n个图形中共有_____ 根火柴(用含n的式子表示);
(3)请计算第2013个图形中共有多少根火柴?
科目:初中数学 来源: 题型:
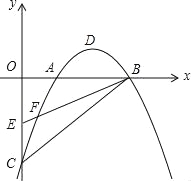
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,﹣1),该抛物线与BE交于另一点F,连接BC.
(1)求该抛物线的解析式,并用配方法把解析式化为y=a(x﹣h)2+k的形式;
(2)若点H(1,y)在BC上,连接FH,求△FHB的面积;
(3)一动点M从点D出发,以每秒1个单位的速度平沿行与y轴方向向上运动,连接OM,BM,设运动时间为t秒(t>0),在点M的运动过程中,当t为何值时,∠OMB=90°?
(4)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是AB上任一点,∠ABC=∠ABD,从下列各条件中补充一个条件,不一定能推出ΔAPC≌ΔAPD的是( )

A.BC=BD B.∠ACB=∠ADB C.AC=AD D.∠CAB=∠DAB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据了解,受到台风“海马”的影响,潮阳区金灶镇农作物受损面积约达35800亩,将数35800用科学记数法可表示为( )
A.0.358×105
B.3.58×104
C.35.8×103
D.358×102
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0,![]() ),点A坐标为(﹣1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(﹣1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数关系表达式.
(2)点F为线段AC上一动点,过F作FE⊥x轴,FG⊥y轴,垂足分别为E、G,当四边形OEFG为正方形时,求出F点的坐标.
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示有理数a、b,点A与原点O两点之间的 距离表示为AO,则AO=|a-0|=|a|,类似地,点B与原点O两点之间的距离表示 为BO,则BO=|b|,点A与点B两点之间的距离表示为AB=|a-b|.请结合数轴,思考并回答以下问题:
(1)①数轴上表示1和-3的两点之间的距离是__________;
②数轴上表示m和-1的两点之间的距离是__________;
③数轴上表示m和-1的两点之间的距离是3,则有理数m是___________;
(2)若x表示一个有理数,并且x比-3大,x比1小,则|x-1|+|x+3|=______;
(3)求满足|x-2|+|x+4|=6的所有整数x的和.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com