
【题目】如图,五边形ABCDE中,AB⊥BC,AE∥CD,∠A=∠E=120°,AB=CD=1,AE=2,则五边形ABCDE的面积等于. 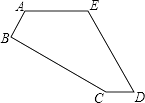
【答案】![]()
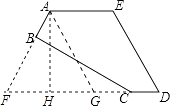
【解析】解:延长DC,AB交于点F,作AG∥DE交DF于点G. ∵AE∥CD,∠A=∠E=120°,
∴四边形AFDE是等腰梯形,且∠F=∠D=60°,△AFG是等边三角形,四边形AGDE是平行四边形.
设BF=x,
∵在直角△BCF中,∠BCF=90°﹣∠F=30°
∴FC=2x,
∴FD=2x+1.
∵平行四边形AGDE中,DG=AE=2,
∴FG=2x﹣1,
∵△AFG是等边三角形中,AF=FG,
∴x+1=2x﹣1,
解得:x=2.
在直角△BCF中,BC=BFtanF=2 ![]() ,
,
则S△BCF= ![]() BFBC=
BFBC= ![]() ×2×2
×2×2 ![]() =2
=2 ![]() .
.
作AH⊥DF于点H.
则AH=AFsinF=3× ![]() =
= ![]() ,
,
则S梯形AFDE= ![]() (AE+DF)AH=
(AE+DF)AH= ![]() ×(2+5)
×(2+5) ![]() =
= ![]() .
.
∴S五边形ABCDE=S梯形AFDE﹣S△BCF= ![]() ﹣2
﹣2 ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】根据题目的已知条件,利用含30度角的直角三角形和勾股定理的概念的相关知识可以得到问题的答案,需要掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AD,CE为△ABC的角平分线且交于O点,∠DAC=30°,∠ECA=35°,则∠ABO等于( )

A. 25° B. 30° C. 35° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由若干个完全相同的小正方体组成的一个几何体.
(1)请画出这个几何体的左视图和俯视图;(用阴影表示)
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和左视图不变,那么最多可以再添加几个小正方体?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)(﹣2,1),先将△ABC沿一确定方向平移得到△A1B1C1 , 点B的对应点B1的坐标是(1,2),再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2 , 点A1的对应点为点A2 . 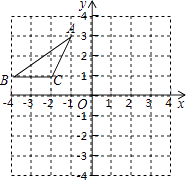
(1)画出△A1B1C1;
(2)画出△A2B2C2;
(3)求出在这两次变换过程中,点A经过点A1到达A2的路径总长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC中,∠ACB=90°,AB=5,BC=3,点D在边AB的延长线上,BD=3,过点D作DE⊥AB,与边AC的延长线相交于点E,以DE为直径作⊙O交AE于点F. 
(1)求⊙O的半径及圆心O到弦EF的距离;
(2)连接CD,交⊙O于点G(如图2).求证:点G是CD的中点. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九(1)、九(2)两班的班长交流了为四川雅安地震灾区捐款的情况:
(1)九(1)班班长说:“我们班捐款总数为1200元,我们班人数比你们班多8人.”
(2)九(2)班班长说:“我们班捐款总数也为1200元,我们班人均捐款比你们班人均捐款多20%.” 请根据两个班长的对话,求这两个班级每班的人均捐款数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥DC,∠B=90°,且AB=10,BC=6,CD=2.点E从点B出发沿BC方向运动,过点E作EF∥AD交边AB于点F.将△BEF沿EF所在的直线折叠得到△GEF,直线FG、EG分别交AD于点M、N,当EG过点D时,点E即停止运动.设BE=x,△GEF与梯形ABCD的重叠部分的面积为y.
(1)证明△AMF是等腰三角形;
(2)当EG过点D时(如图(3)),求x的值;
(3)将y表示成x的函数,并求y的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com