
 如图,△ABC中,AB=2,AC=3,1<BC<5,分别以AB、BC、AC为边向外作正方形ABIH、BCDE和正方形ACFG,则图中阴影部分的最大面积为( )
如图,△ABC中,AB=2,AC=3,1<BC<5,分别以AB、BC、AC为边向外作正方形ABIH、BCDE和正方形ACFG,则图中阴影部分的最大面积为( )| A. | 6 | B. | 9 | C. | 11 | D. | 无法计算 |
分析 有旋转的性质得到CB=BE=BH′,推出C、B、H'在一直线上,且AB为△ACH'的中线,得到S△BEI=S△ABH′=S△ABC,同理:S△CDF=S△ABC,当∠BAC=90°时,即sin∠BAC=1,S△ABC的面积最大,S△BEI=S△CDF=S△ABC最大,推出S△GBI=S△ABC,于是得到阴影部分面积之和为S△ABC的3倍,于是得到结论.
解答 解: 把△IBE绕B顺时针旋转90°,使BI与AB重合,E旋转到H'的位置,
把△IBE绕B顺时针旋转90°,使BI与AB重合,E旋转到H'的位置,
∵四边形BCDE为正方形,∠CBE=90°,CB=BE=BH′,
∴C、B、H'在一直线上,且AB为△ACH'的中线,
∴S△BEI=S△ABH′=S△ABC,
同理:S△CDF=S△ABC,
∵S△ABC=$\frac{1}{2}$AB•AC•sin∠BAC=$\frac{1}{2}$×2×3sin∠BAC=3sin∠BAC,
∴当∠BAC=90°时,
即sin∠BAC=1,S△ABC的面积最大,
S△BEI=S△CDF=S△ABC最大,
∵∠ABC=∠CBG=∠ABI=90°,
∴∠GBE=90°,
∴S△GBI=S△ABC,
所以阴影部分面积之和为S△ABC的3倍,
又∵AB=2,AC=3,
∴图中阴影部分的最大面积为3×$\frac{1}{2}$×2×3=9,
故选B.
点评 本题考查了勾股定理,利用了旋转的性质:旋转前后图形全等得出图中阴影部分的最大面积是S△ABC的3 倍是解题关键.


科目:初中数学 来源: 题型:填空题
 如图,在一个正方形被分成二十六个面积均为1的小正方形,点A与点B在两个格点上,问在格点上是否存在一个点C,使△ABC为等腰三角形,这样的点有5个.
如图,在一个正方形被分成二十六个面积均为1的小正方形,点A与点B在两个格点上,问在格点上是否存在一个点C,使△ABC为等腰三角形,这样的点有5个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
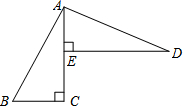 已知:如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.
已知:如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,下列条件中:①∠1=∠2;②∠3=∠4;③∠5=∠D;④∠1=∠6;⑤∠BAD+∠D=180°;⑥∠BCD+∠D=180°
如图,下列条件中:①∠1=∠2;②∠3=∠4;③∠5=∠D;④∠1=∠6;⑤∠BAD+∠D=180°;⑥∠BCD+∠D=180°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 光大路桥公司中标承包了一段路基工程,进入施工场地后,所挖路基的长度y(m)与工作时间x(天)之间的函数关系如图所示,请根据提供的信息解答下列问题:
光大路桥公司中标承包了一段路基工程,进入施工场地后,所挖路基的长度y(m)与工作时间x(天)之间的函数关系如图所示,请根据提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com