
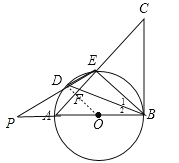
【题目】如图,AB是⊙O的直径,点D是![]() 上一点,且∠BDE=∠CBE,BD与AE交于点F.
上一点,且∠BDE=∠CBE,BD与AE交于点F.
(1)求证:BC是⊙O的切线;
(2)若BD平分∠ABE,求证:![]() =DFDB;
=DFDB;
(3)在(2)的条件下,延长ED、BA交于点P,若PA=AO,DE=2,求PD的长.

【答案】(1)证明见解析;(2)证明见解析;(3)4.
【解析】
试题分析:(1)利用圆周角定理得到∠AEB=90°,∠EAB=∠BDE,而∠BDE=∠CBE,则∠CBE+∠ABE=90°,则根据切线的判定方法可判断BC是⊙O的切线;
(2)证明△DFE∽△DEB,然后利用相似比可得到结论;’
(3)连结DE,先证明OD∥BE,则可判断△POD∽△PBE,然后利用相似比可得到关于PD的方程,再解方程求出PD即可.
试题解析:(1)证明:∵AB是⊙O的直径,∴∠AEB=90°,∴∠EAB+∠ABE=90°,∵∠EAB=∠BDE,∠BDE=∠CBE,∴∠CBE+∠ABE=90°,即∠ABC=90°,∴AB⊥BC,∴BC是⊙O的切线;
(2)证明:∵BD平分∠ABE,∴∠1=∠2,而∠2=∠AED,∴∠AED=∠1,∵∠FDE=∠EDB,∴△DFE∽△DEB,∴DE:DF=DB:DE,∴![]() =DFDB;
=DFDB;
(3)连结DE,如图,∵OD=OB,∴∠2=∠ODB,而∠1=∠2,∴∠ODB=∠1,∴OD∥BE,∴△POD∽△PBE,∴![]() ,∵PA=AO,∴PA=AO=BO,∴
,∵PA=AO,∴PA=AO=BO,∴![]() ,即
,即![]() ,∴PD=4.
,∴PD=4.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:
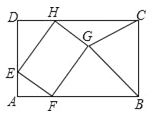
【题目】如图,矩形ABCD中,AD=6,CD=6+![]() ,E为AD上一点,且AE=2,点F,H分别在边AB,CD上,四边形EFGH为矩形,点G在矩形ABCD的内部,则当△BGC为直角三角形时,AF的值是 .
,E为AD上一点,且AE=2,点F,H分别在边AB,CD上,四边形EFGH为矩形,点G在矩形ABCD的内部,则当△BGC为直角三角形时,AF的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司要把3000吨货物从M市运到W市.(每日的运输量为固定值)
(1)从运输开始,每天运输的货物吨数y(单位:吨)与运输时间x(单位:天)之间有怎样的函数关系式?
(2)因受到沿线道路改扩建工程影响,实际每天的运输量比原计划少20%,以致推迟1天完成运输任务,求原计划完成运输任务的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(﹣2,a),B(1,b)是一次函数y=﹣2x+1图象上的两个点,则a与b的大小关系是( )
A.a>bB.a<bC.a=bD.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在边长为a的正方形中,画出两个长方形阴影,则阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的长是 ,宽是 ,面积是 (写成多项式乘法的形式);
(3)比较左、右两图的阴影部分面积,可以得到乘法公式 (用式子表达);
(4)运用你所得到的公式计算:
①10.3×9.7
②(2m+n﹣p)(2m﹣n+p)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com