
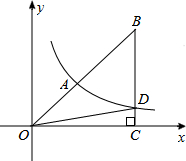
 如图,双曲线y=
如图,双曲线y=| k |
| x |
| AO |
| AB |
| 2 |
| 3 |
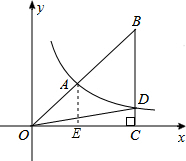 解:过A作AE⊥x轴于点E.
解:过A作AE⊥x轴于点E.| S△OAE |
| S△OBC |
| S△OAE |
| S△OAE+S四边形AECB |
| AO |
| OB |
| 4 |
| 25 |


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
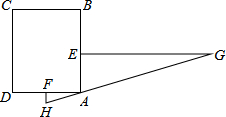 “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=
“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com