Question

13．如图1，在矩形ABCD中，AB＜BC，AC，BD交于点O．点E为线段AC上的一个动点，连接DE，BE，过E作EF⊥BD于F．设AE=x，图1中某条线段的长为y，若表示y与x的函数关系的图象大致如图2所示，则这条线段可能是图1中的（　　）

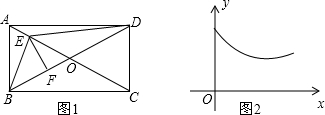
• A． 线段EF
• B． 线段BE
• C． 线段DE
• D． 线段CE

Answer 1

分析 作BN⊥AC，垂足为N，FM⊥AC，垂足为M，DG⊥AC，垂足为G，分别找出线段EF、CE、BE最小值出现的时刻即可得出结论．

解答 解：如图，作BN⊥AC，垂足为N，FM⊥AC，垂足为M，DG⊥AC，垂足为G．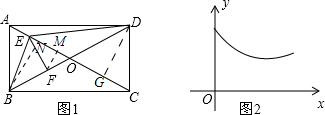

由垂线段最短可知：当点E与点M重合时，即AE＜$\frac{1}{2}$AC时，FE有最小值，与函数图象不符，故A错误；
由垂线段最短可知：当点E与点N重合时，即AE＜$\frac{1}{2}$AC时，BE有最小值，与函数图象不符，故B错误；
由垂线段最短可知：当点E与点G重合时，即AE＞$\frac{1}{2}$AC时，DE有最小值，故C正确；
∵CE=AC-AE，CE随着AE的增大而减小，故D错误；
故选：C．

点评 本题主要考查的是动点问题的函数图象，根据垂线段最短确定出函数最小值出现的时刻是解题的关键．