
【题目】如图,已知抛物线y=ax2+bx+c经过A(﹣2,0),B(4,0),C(0,3)三点.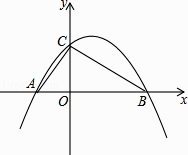
(1)求该抛物线的解析式;
(2)在y轴上是否存在点M,使△ACM为等腰三角形?若存在,请直接写出所有满足要求的点M的坐标;若不存在,请说明理由;
(3)若点P(t,0)为线段AB上一动点(不与A,B重合),过P作y轴的平行线,记该直线右侧与△ABC围成的图形面积为S,试确定S与t的函数关系式.
【答案】
(1)
解:把A(﹣2,0),B(4,0),C(0,3)代入抛物线y=ax2+bx+c得:
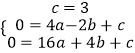 ,解得:
,解得: 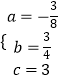 ,
,
则抛物线的解析式是:y=﹣ ![]() x2+
x2+ ![]() x+3
x+3
(2)
解:如图1,作线段CA的垂直平分线,交y轴于M,交AC与N,连结AM1,则△AM1C是等腰三角形,
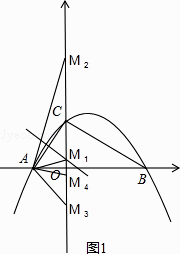
∵AC= ![]() =
= ![]() ,
,
∴CN= ![]() ,
,
∵△CNM1∽△COA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴CM1= ![]() ,
,
∴OM1=OC﹣CM1=3﹣ ![]() =
= ![]() ,
,
∴M1的坐标是(0, ![]() ),
),
当CA=CM2= ![]() 时,则△AM2C是等腰三角形,
时,则△AM2C是等腰三角形,
则OM2=3+ ![]() ,
,
M2的坐标是(0,3+ ![]() ),
),
当CA=AM3= ![]() 时,则△AM3C是等腰三角形,
时,则△AM3C是等腰三角形,
则OM3=3,
M3的坐标是(0,﹣3),
当CA=CM4= ![]() 时,则△AM4C是等腰三角形,
时,则△AM4C是等腰三角形,
则OM4= ![]() ﹣3,
﹣3,
M4的坐标是(0,3﹣ ![]() ),
),
(3)
解:如图2,当点P在y轴或y轴右侧时,
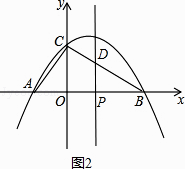
设直线与BC交于点D,
∵OB=4,OC=3,
∴S△BOC=6,
∵BP=BO﹣OP=4﹣t,
∴ ![]() =
= ![]() ,
,
∵△BPD∽△BOC,
∴ ![]() =(
=( ![]() )2,
)2,
∴ ![]() =(
=( ![]() )2,
)2,
∴S=S△BPD= ![]() t2﹣3t+6(0≤t<4);
t2﹣3t+6(0≤t<4);
当点P在y轴左侧时,
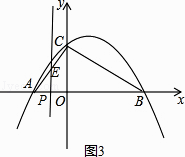
设直线与AC交与点E,
∵OP=﹣t,AP=t+2,
∴ ![]() =
= ![]() ,
,
∵ ![]() =(
=( ![]() )2,
)2,
∴ ![]() =(
=( ![]() )2,
)2,
∴S△APE= ![]() ,
,
∴S=S△ABC﹣S△APE=9﹣ ![]() =﹣
=﹣ ![]() t2﹣3t+6(﹣2<t<0).
t2﹣3t+6(﹣2<t<0).
【解析】(1)把A(﹣2,0),B(4,0),C(0,3)代入抛物线y=ax2+bx+c,求解即可;(2)作线段CA的垂直平分线,交y轴于M,交AC与N,连结AM1 , 则△AM1C是等腰三角形,然后求出OM1得出M1的坐标,当CA=CM2时,则△AM2C是等腰三角形,求出OM2得出M2的坐标,当CA=AM3时,则△AM3C是等腰三角形,求出OM3得出M3的坐标,当CA=CM4时,则△AM4C是等腰三角形,求出OM4得出M4的坐标,(3)当点P在y轴或y轴右侧时,设直线与BC交与点D,先求出S△BOC , 再根据△BPD∽△BOC,得出 ![]() =(
=( ![]() )2 ,
)2 , ![]() =(
=( ![]() )2 , 求出S=S△BPD;当点P在y轴左侧时,设直线与AC交与点E,根据
)2 , 求出S=S△BPD;当点P在y轴左侧时,设直线与AC交与点E,根据 ![]() =(
=( ![]() )2 , 得出
)2 , 得出 ![]() =(
=( ![]() )2 , 求出S=S△ABC﹣S△APE=9﹣
)2 , 求出S=S△ABC﹣S△APE=9﹣ ![]() ,再整理即可.
,再整理即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
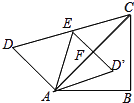
【题目】如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB= 6![]() cm,点D′到BC的距离是( )
cm,点D′到BC的距离是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
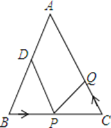
【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点![]() 如果点P在线段BC上以v厘米
如果点P在线段BC上以v厘米![]() 秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动
秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动![]() 若点Q的运动速度为3厘米
若点Q的运动速度为3厘米![]() 秒,则当△BPD与△CQP全等时,v的值为( )
秒,则当△BPD与△CQP全等时,v的值为( )
A. 2.5 B. 3 C. 2.25或3 D. 1或5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,然后回答问题:
解方程: ![]()
解:①当![]() ≥0时,原方程可化为:
≥0时,原方程可化为: ![]() ,解得
,解得![]() ;
;
②当![]() <0时,原方程可化为:
<0时,原方程可化为: ![]() ,解得
,解得![]() ;
;
所以原方程的解是![]() 或
或![]()
(1)解方程: ![]()
(2)探究:当![]() 为何值时,方程
为何值时,方程![]() ①无解;②只有一个解;③有两个解。
①无解;②只有一个解;③有两个解。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1 000元;经粗加工后销售,每吨利润可达4 500元;经精加工后销售,每吨利润涨至7 500元.
当地一家蔬菜公司收获这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节等条件限制,公司必须在15天内将这批蔬菜全部销售或加工完毕,为此公司制订了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多的对蔬菜进行精加工,没有来得及进行加工的蔬菜,在市场上直接销售;
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.
你认为选择哪种方案获利最多?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,∠MON=45°,OA1=1,作正方形A1B1C1A2 , 周长记作C1;再作第二个正方形A2B2C2A3 , 周长记作C2;继续作第三个正方形A3B3C3A4 , 周长记作C3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第n个正方形的周长Cn= . 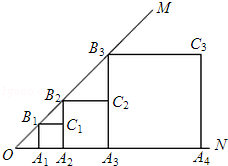
查看答案和解析>>
科目:初中数学 来源: 题型:
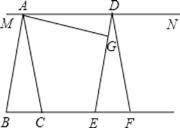
【题目】如图所示,将![]() 沿直线BC方向平移
沿直线BC方向平移![]() 的位置,G是DE上一点,连接AG,过点A、D作直线MN.
的位置,G是DE上一点,连接AG,过点A、D作直线MN.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,判断AG与DE的位置关系,并证明你的结论.
,判断AG与DE的位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
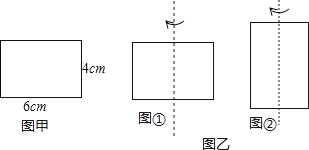
【题目】探究:有一长6cm,宽4cm的矩形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个圆柱,现可按照两种方案进行操作:
方案一:以较长的一组对边中点所在直线为轴旋转,如图①;
方案二:以较短的一组对边中点所在直线为轴旋转,如图②.
(1)请通过计算说明哪种方法构造的圆柱体积大;
(2)如果该矩形的长宽分别是5cm和3cm呢?请通过计算说明哪种方法构造的圆柱体积大;
(3)通过以上探究,你发现对于同一个矩形(不包括正方形),以其一组对边中点所在直线为轴旋转得到一个圆柱,怎样操作所得到的圆柱体积大(不必说明原因)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com