
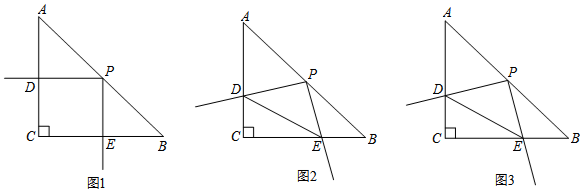
���� ��1������PC�����ݵ���ֱ�������ε����ʣ��ж���DCP�ա�EBP��ASA�������ɵó�PD=PE��
��2������ȫ�������ε����ʵõ�PD=PE���ٸ��ݡ�DPE=90�㣬���ɵõ���PDE�ǵ���ֱ�������Σ�
��3�����ݡ�DCP�ա�EBP���ɵ�S��DCP=S��EBP���ٸ����ı���PDCE�����=S��DCP+S��ECP=S��EBP+S��ECP=S��BCP=$\frac{1}{2}$S��ABC���м��㼴�ɣ�
��4���ȸ���S��DPE=S��DCE��DE=2$\sqrt{2}$�����S��DCE=2����DC=x��CE=y����BE=x������Rt��DCE�У�$\frac{1}{2}$xy=2��x2+y2=��2$\sqrt{2}$��2���ɵã�x+y��2=16���ݴ˿ɵ�x+y=4����BE+CE=4�������õ�a��ֵ��
��� 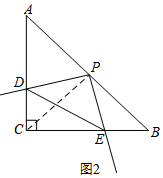 �⣺��1������PC��
�⣺��1������PC��
�ߡ�ABC�У���C=90�㣬AC=BC=a��PΪAB���е㣬
��CP��AB��CP=$\frac{1}{2}$AB=BP����DCP=��B=45�㣬
�ߡ�DPE=90�㣬
���DPC=��EPB��
�ڡ�DCP�͡�EBP�У�
$\left\{\begin{array}{l}{��DPC=��EPB}\\{CP=BP}\\{��DCP=��B}\end{array}\right.$��
���DCP�ա�EBP��ASA����
��PD=PE��CD=BE��
�ʴ�Ϊ��PD=PE��
��2����PDE����״Ϊ����ֱ�������Σ�
֤�����ɣ�1���ɵã�PD=PE��
�֡ߡ�DPE=90�㣬
���PDE�ǵ���ֱ�������Σ�
��3���ı���PDCE������������仯��
���ɣ��ɣ�1���ɵã���DCP�ա�EBP��
��S��DCP=S��EBP��
���ı���PDCE�����=S��DCP+S��ECP=S��EBP+S��ECP=S��BCP=$\frac{1}{2}$S��ABC=$\frac{1}{2}$��$\frac{1}{2}$a2=$\frac{1}{4}$a2��
���ı���PDCE�����Ϊ��ֵ$\frac{1}{4}$a2��
��4����ͼ3���ߡ�PDE�ǵ���ֱ�������Σ�DE=2$\sqrt{2}$��
��DP=EP=2��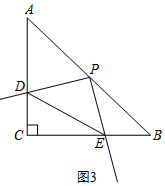
��S��DPE=$\frac{1}{2}$��2��2=2��
��S��DCE=2��
��DC=x��CE=y����BE=x��
��Rt��DCE��$\frac{1}{2}$xy=2��x2+y2=��2$\sqrt{2}$��2��
�ࣨx+y��2=16��
��x+y��0��
��x+y=4��
��BE+CE=4��
��a��ֵΪ4��
���� ���������������ۺ��⣬��Ҫ�����˵���ֱ�������ε��ж������ʣ�ȫ�������ε��ж��������Լ����ɶ������ۺ�Ӧ�ã��������Ĺؼ����������߹���ȫ�������Σ�����ȫ�������εĶ�Ӧ����Ƚ�����⣮����ʱע�⣬����ֱ����������һ������������Σ��������������ε����ʣ����߱����������κ�ֱ�������ε��������ʣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | -2 | C�� | -1 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
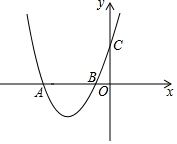
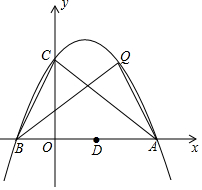 ��ͼ��������y=ax2-2ax+c��a��0����y���ཻ�ڵ�C��0��4������x���ཻ��A��B���㣬��A������Ϊ��4��0����
��ͼ��������y=ax2-2ax+c��a��0����y���ཻ�ڵ�C��0��4������x���ཻ��A��B���㣬��A������Ϊ��4��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
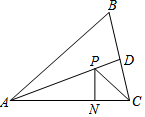 ��ͼ���ڡ�ABC�У���BAC=60�㣬AD�ǡ�BAC��ƽ���ߣ�AC=$\sqrt{6}$������P��AD��һ���㣬����PN��AC�ڵ�N����PN+PC����Сֵ��$\frac{3\sqrt{2}}{2}$��
��ͼ���ڡ�ABC�У���BAC=60�㣬AD�ǡ�BAC��ƽ���ߣ�AC=$\sqrt{6}$������P��AD��һ���㣬����PN��AC�ڵ�N����PN+PC����Сֵ��$\frac{3\sqrt{2}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������M��y=��x+1����x+a����a��1����x����A��B���㣨A��B����ߣ�����y����C�㣮������M����y��ԳƵ�������N��x����P��Q���㣨P��Q����ߣ�
��ͼ��������M��y=��x+1����x+a����a��1����x����A��B���㣨A��B����ߣ�����y����C�㣮������M����y��ԳƵ�������N��x����P��Q���㣨P��Q����ߣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com