
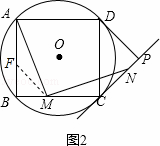
如图,四边形ABCD是⊙O的内接正方形,AB=4,PC、PD是⊙O的两条切线,C、D为切点.
(1)如图1,求⊙O的半径;
(2)如图1,若点E是BC的中点,连接PE,求PE的长度;
(3)如图2,若点M是BC边上任意一点(不含B、C),以点M为直角顶点,在BC的上方作∠AMN=90°,交直线CP于点N,求证:AM=MN.
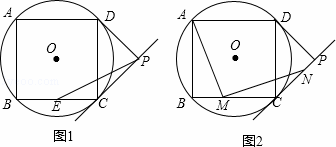
解:(1)如图1,连接OD,OC,
∵PC、PD是⊙O的两条切线,C、D为切点,
∴∠ODP=∠OCP=90°,
∵四边形ABCD是⊙O的内接正方形,
∴∠DOC=90°,OD=OC,
∴四边形DOCP是正方形,
∵AB=4,∠ODC=∠OCD=45°,
∴DO=CO=DC•sin45°=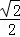 ×4=2
×4=2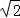 ;
;
(2)如图1,连接EO,OP,
∵点E是BC的中点,
∴OE⊥BC,∠OCE=45°,
则∠E0P=90°,
∴EO=EC=2,OP=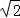 CO=4,
CO=4,
∴PE=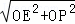 =2
=2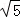 ;
;
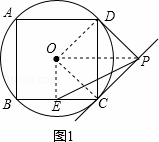
(3)证明:如图2,在AB上截取BF=BM,
∵AB=BC,BF=BM,
∴AF=MC,∠BFM=∠BMF=45°,
∵∠AMN=90°,
∴∠AMF+∠NMC=45°,∠FAM+∠AMF=45°,
∴∠FAM=∠NMC,
∵由(1)得:PD=PC,∠DPC=90°,
∴∠DCP=45°,
∴∠MCN=135°,
∵∠AFM=180°﹣∠BFM=135°,
在△AFM和△CMN中
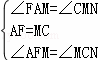 ,
,
∴△AFM≌△CMN(ASA),
∴AM=MN.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
现有三张反面朝上的扑克牌:红桃2、红桃3、黑桃x(1≤x≤13且x为奇数或偶数).把牌洗匀后第一次抽取一张,记好花色和数字后将牌放回,重新洗匀第二次再 抽取一张.
抽取一张.
(1)求两次抽得相同花色的概率;
(2)当甲选择x为奇数,乙选择x为偶数时,他们两次抽得的数字和是奇数的可能性大小一样吗?请说明理由.(提示:三张扑克牌可以分别简记为红2、红3、黑x)
查看答案和解析>>
科目:初中数学 来源: 题型:
下列因式分解正确的是( )
A. x2﹣4=(x+4)(x﹣4) B. x2+2x+1=x(x+2)+1
C. 3mx﹣6my=3m(x﹣6y) D. 2x+4=2(x+2)
查看答案和解析>>
科目:初中数学 来源: 题型:
2015年,我国筹备成立亚洲基础设旌投资银行(亚投行)。据统计,2010年至2020
年,亚洲各经济体的基础设施如果要达到世界平均水平,至少需要8 000 000 000 000
美元基建投资,将8 000 000 000 000用科学记效法表示应为 ( )
A. 08×1013 B.8×l013 C.8×1012 D.80×l011
查看答案和解析>>
科目:初中数学 来源: 题型:
如右图,点A(1,6)和点M(m,n)都在反比例函数y= k (k>0)的图像上.
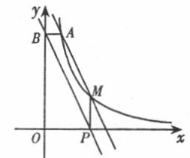
(1)求k的值;
(2)当m=3时,求直线AM的解析式;
(3)当m>1时,过点M作MP上x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com