
如右图,点A(1,6)和点M(m,n)都在反比例函数y= k (k>0)的图像上.
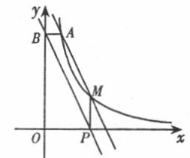
(1)求k的值;
(2)当m=3时,求直线AM的解析式;
(3)当m>1时,过点M作MP上x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.
解:(1)点A(1,6)在反比例函数y=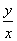 (k>o)的图像上,所以k=xy=6………………2分
(k>o)的图像上,所以k=xy=6………………2分
(2)当m=3时,则n=2,所以M(3,2)……………3分
设直线AM的解析式为y=kx+b
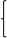 6=k+b
6=k+b
则 2=3k+b …………4分
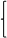 解得k=-2
解得k=-2
B=8
所以直线AM的解析式为y=-2x+8……………………5分
(3)延长BA、PM相交于N则∠N =90°…………………6分
∵A(1,6),M(m,n)
∴B(0,6),P(m,0),N(m,6)
∴BN=m,PN=6,AN=m-1,MN=6-n……………… 7分
∴tan∠1= =
=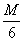 , tan∠2=
, tan∠2= 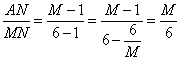
∴tan∠1=tan∠2……………… 8分
∴∠1=∠2
∴AM//BP………………………………9分


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
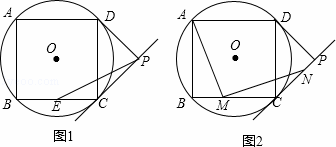
如图,四边形ABCD是⊙O的内接正方形,AB=4,PC、PD是⊙O的两条切线,C、D为切点.
(1)如图1,求⊙O的半径;
(2)如图1,若点E是BC的中点,连接PE,求PE的长度;
(3)如图2,若点M是BC边上任意一点(不含B、C),以点M为直角顶点,在BC的上方作∠AMN=90°,交直线CP于点N,求证:AM=MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
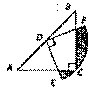
如右图,在△ABC中.CA = CB,∠ACB= 90°.AB=2.点D为AB 的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF 上,则图中阴影部分的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为__________________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
据悉,世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000 00007克,用科学记数法表示此数正确的是( )
00007克,用科学记数法表示此数正确的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下列内容,设a,b,c是一个三角形的三条边的长,且a是最长边,我们可以利用a,b,c三边长间的关系来判断这个三角形的形状:
①若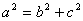 ,则该三角形是直角三角形;②若
,则该三角形是直角三角形;②若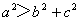 ,则该三角形是钝角三角形;③
,则该三角形是钝角三角形;③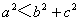 ,则该三角形是锐角三角形
,则该三角形是锐角三角形
例如一个三角形的三边长分别是4,5,6,则最长边是6,由于 ,故由上
,故由上 面③可知该三角形是锐角三角形,请解答以下问题
面③可知该三角形是锐角三角形,请解答以下问题
(1)若一个三角形的三条边长分别是2,3,4,则该三角形是 三角形
( 2)若一个三角形的三条边长分别是3,4,x且这个三角形是直角三角形,则x的值为
2)若一个三角形的三条边长分别是3,4,x且这个三角形是直角三角形,则x的值为
(3)若一个三角形的三条边长分别是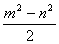 ,
,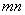 ,
,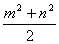 请判断这个三角形的形状,并写出你的判断过程
请判断这个三角形的形状,并写出你的判断过程
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com