
 为筹备2014年元旦晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图所示,已知圆筒高108cm,其横截面周长为36cm,如果在圆筒表面恰好能缠绕油纸4圈,应至少裁剪180cm的油纸.
为筹备2014年元旦晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图所示,已知圆筒高108cm,其横截面周长为36cm,如果在圆筒表面恰好能缠绕油纸4圈,应至少裁剪180cm的油纸. 分析 将圆柱体沿一条母线展开,可得图形,如下图,只需求出每一圈所需的油纸的长度即可,展开后即转化为求解直角三角形的问题,在Rt△ABC中,AB已知,BC=$\frac{108}{4}$cm,根据勾股定理即可得出AC的长度,由于油纸缠绕4圈,故油纸的总长度为4AC的长度.
解答 解:将圆筒展开后成为一个矩形,如图,整个油纸也随之分成相等4段只需求出AC长即可,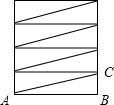 在Rt△ABC中,
在Rt△ABC中,
∵AB=36,BC=$\frac{108}{4}$cm,
∴AC2=AB2+BC2=362+272,
∴AC=45cm,
∴整个油纸的长为45×4=180(cm).
故答案为:180
点评 本题考查的是平面展开-最短路径问题,此类问题应先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| 定价/元 | 1.8 | 2 | 2.3 | 2.5 | 2.8 | 3 |
| 销量/个 | 20 | 25 | 30 | 26 | 22 | 18 |
| A. | 成本价 | B. | 定价 | ||
| C. | 销量 | D. | 以上说法都不正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10$\sqrt{5}$ | B. | 11$\sqrt{5}$ | C. | 12$\sqrt{5}$ | D. | 13$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
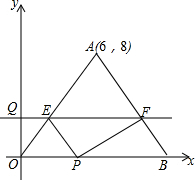 如图,△OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,点P在线段OB上,点Q在y轴的正半轴上,OP=2OQ,过点Q作x轴的平行线分别交OA,AB于点E,F.
如图,△OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,点P在线段OB上,点Q在y轴的正半轴上,OP=2OQ,过点Q作x轴的平行线分别交OA,AB于点E,F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com