
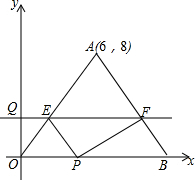
 如图,△OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,点P在线段OB上,点Q在y轴的正半轴上,OP=2OQ,过点Q作x轴的平行线分别交OA,AB于点E,F.
如图,△OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,点P在线段OB上,点Q在y轴的正半轴上,OP=2OQ,过点Q作x轴的平行线分别交OA,AB于点E,F.分析 (1)由A坐标确定出OA的长,即为OB的长,确定出B坐标,利用待定系数法求出直线AB解析式即可;
(2)由A坐标确定出直线OA解析式,设OQ=t,则有OP=2t,表示出E与F坐标,进而表示出EF长,由四边形POEF为平行四边形,得到EF=OP,求出t的值,即可确定出P坐标;
(3)分三种情况考虑:若∠PEF=90°;若∠PFE=90°;若∠EPF=90°,过E、F分别作x轴垂线,垂足分别为G、H,分别求出t的值,确定出满足题意P坐标即可.
解答 解:(1)∵A(6,8),∴OA=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴OB=OA=10,即B(10,0),
设直线AB解析式为y=kx+b,
把A与B坐标代入得:$\left\{\begin{array}{l}{6k+b=8}\\{10k+b=0}\end{array}\right.$,
解得:k=-2,b=20.
则直线AB解析式为y=-2x+20,;
(2)由A(6,8),得到直线OA解析式为y=$\frac{4}{3}$x,
设OQ=t,则有OP=2OQ=2t,
把y=t代入y=$\frac{4}{3}$x得:x=$\frac{3}{4}$t;代入y=-2x+20得:x=10-$\frac{1}{2}$t,
∴E($\frac{3}{4}$t,t),F(10-$\frac{1}{2}$t,t),
∴EF=10-$\frac{1}{2}$t-$\frac{3}{4}$t=10-$\frac{5}{4}$t,
若四边形POEF为平行四边形,则有EF=OP,即10-$\frac{5}{4}$t=2t,
解得:t=$\frac{40}{13}$;
(3)分三种情况考虑:
若∠PEF=90°,则有$\frac{3}{4}$t=2t,无解,不可能;
若∠PFE=90°,则有10-$\frac{t}{2}$=2t,解得:t=4,此时OP=8,即P(8,0);
若∠EPF=90°,过E、F分别作x轴垂线,垂足分别为G、H,
∴Rt△EGP∽Rt△PHF,
∴$\frac{EG}{GP}$=$\frac{PH}{HF}$,即$\frac{t}{2t-\frac{3}{4}t}$=$\frac{10-\frac{1}{2}t-2t}{t}$,
解得:t=$\frac{100}{33}$,此时P=$\frac{200}{33}$,即P($\frac{200}{33}$,0).
综上,P的坐标为(8,0)或($\frac{200}{33}$,0).
点评 此题属于一次函数综合题,涉及的知识有:坐标与图形性质,勾股定理,待定系数法确定一次函数解析式,以及平行四边形的性质,熟练掌握待定系数法是解本题的关键.


科目:初中数学 来源: 题型:填空题
 为筹备2014年元旦晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图所示,已知圆筒高108cm,其横截面周长为36cm,如果在圆筒表面恰好能缠绕油纸4圈,应至少裁剪180cm的油纸.
为筹备2014年元旦晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图所示,已知圆筒高108cm,其横截面周长为36cm,如果在圆筒表面恰好能缠绕油纸4圈,应至少裁剪180cm的油纸.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com