
【题目】A水果超市最近新进了一批百香果,每斤进价10元,为了合理定价,在第一周试行机动价格,卖出时每斤以15元为标准,超出15元的部分记为正,不足15元的部分记为负,超市记录第一周百香果的售价情况和售出情况:

(1)第一周星期三超市售出的百香果单价为_______元,这天的利润是_____元.
(2)第一周超市出售此种百香果的收益如何?(盈利或亏损的钱数)
(3)超市为了促销这种百香果,决定从下周一起推出两种促销方式:
方式一:购买不超过5斤百香果,每斤20元,超出5斤的部分,每斤降价4元;
方式二:每斤售价17元.
林老师决定下周在A水果超市购买40斤百香果,通过计算说明应选择上述两种促销方式中的哪种方式购买更省钱.
【答案】(1)15,50;(2)第一周超市出售此种百香果盈利600元;(3)选择方式一购买更省钱,见解析
【解析】
(1)根据题意和表格计算即可;
(2)先计算出第一周超市每天售出百香果的单价,然后计算出每天的利润求和即可;
(3)根据题意,分别计算出方式一和方式二各需多少钱,即可判断.
解:(1)根据题意:第一周星期三超市售出的百香果单价为:15+0=15元,这天的利润是:(15-10)×10=50元.
(2)第一周超市每天售出百香果的单价依次为:
16元、13元、15元、14元、17元、20元、11元
(16-10)×20+(13-10)×35+(15-10)×10+(14-10)×30+(17-10)×15+(20-10)×5+(11-10)×50=600(元);
所以第一周超市出售此种百香果盈利600元
(3)方式一:(40-5)×(20-4)+20×5=660(元)
方式二:40×17=680(元)
∵660<680,
答:选择方式一购买更省钱.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
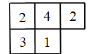
【题目】根据要求画图,并回答问题:如图是一些小方块所搭几何体的俯视图,俯视图的每个小正方形中的数字表示该位置的小方块的个数,
①请在右边的网格中画出这个几何体的主视图和左视图;
②如果每个小正方体的棱长为1,则该几何体的表面积为
③在不改变俯视图、主视图、左视图的情况下,最多能添加 个小方块.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从仓库O出发在东西街道上运送水果,规定向东为正方向,一次到达的5个销售地点依次分别为A,B,C,D,E,最后回到仓库O,货车行驶的记录(单位:千米)如下:+1,+3,﹣6,﹣1,﹣2,+5.请问:
(1)请以仓库O为原点,向东为正方向,选择适当的单位长度,画出数轴,并标出A,B,C,D,E的位置;
(2)试求出该货车共行驶了多少千米?
(3)如果货车运送的水果以100千克为标准重量,超过的千克数记为正数,不足的千克数记为负数,则运往A,B,C,D,E五个地点的水果重量可记为:
+50,﹣15,+25,﹣10,﹣15,则该货车运送的水果总重量是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,他从A处出发去看望B、C、D处的其他甲虫,规定:向上向右走均为正,向下向左走均为负,如果从A到B记为A→B{1,4},从B到A记为:B→A{﹣1,﹣4},其中第一个数表示左右方向,第二个数表示上下方向.
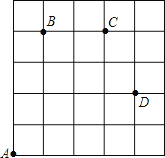
(1)图中A→C{ , },C→B{ , }.
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程.
(3)若图中另有两个格点M、N,且M→A{2﹣a,b﹣3},M→N{3﹣a,b﹣2},则N→A应记为什么?直接写出你的答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
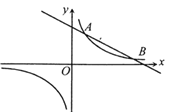
【题目】如图,反比例函数y=![]() 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
(1)求反比例函数与一次函数的表达式;
(2)点E为y轴上一个动点,若S△AEB=10,求点E的坐标.
(3)结合图像写出不等式![]() 的解集;
的解集;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B在数轴上分别表示a,b.请认真观察数轴及表格再解答问题:
![]()

(1)表格中的m=_____,n=________
(2)若A、B两点间的距离记为d,则d与a、b间的等量关系为__________
(3)结合上述结论,并利用数轴解答下列问题
①满足到表示数4和-6的点的距离之和等于16的数为
②若点C表示的数为x,求![]() 的最小值.(本页可作为草稿纸使用)
的最小值.(本页可作为草稿纸使用)
查看答案和解析>>
科目:初中数学 来源: 题型:
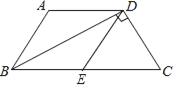
【题目】已知:如图,四边形ABCD中,AD∥BC,对角线BD平分∠ABC,且BD⊥DC,E为BC中点,AB=DE.
(1)求证:四边形ABED是菱形;
(2)若∠C=60°,CD=4,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与函数y=![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.
(1)求m,k,n的值;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 的两边分别平行.
的两边分别平行.
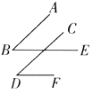
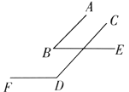
① ②
(1)在图①中,![]() 与
与![]() 的数量关系是什么?为什么?
的数量关系是什么?为什么?
(2)在图②中,![]() 与
与![]() 的数量关系是什么?为什么?
的数量关系是什么?为什么?
(3)由(1)(2)可得结论:________;
(4)应用:若两个角的两边两两互相平行,其中一个角比另一个角的2倍少![]() ,求这两个角的度数.
,求这两个角的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com