
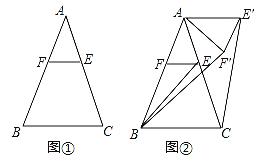
【题目】已知,△ABC中,AB=AC,点E是边AC上一点,过点E作EF∥BC交AB于点F
(1)如图①,求证:AE=AF;
(2)如图②,将△AEF绕点A逆时针旋转α(0°<α<144°)得到△AE′F′.连接CE′BF′.
①若BF′=6,求CE′的长;
②若∠EBC=∠BAC=36°,在图②的旋转过程中,当CE′∥AB时,直接写出旋转角α的大小.
【答案】(1)答案见解析;(2)①6;②36°或72°.
【解析】试题分析:(1)根据等腰三角形两底角相等∠B=∠C,再根据平行线的性质得出,∠AFE=∠A,∠AEF=∠C,得出∠AFE=∠AEF,进一步得出结论;
(2)求出AE=AF,再根据旋转的性质可得∠E′AC=∠F′AB,AE′=AF′,然后利用“边角边”证明△CAE′和△BAF′全等,根据全等三角形对应边相等证明即可;
(3)把△AEF绕点A逆时针旋转AE′与过点C与AB平行的直线相交于M、N,然后分两种情况,根据等腰梯形的性质和等腰三角形的性质分别求解即可.
试题解析:(1)证明:∵AB=AC,
∴∠ABC=∠C,
∵EF∥BC,
∴∠AFE=∠A,∠AEF=∠C,
∴∠AFE=∠AEF,
∴AE=AF.
(2)①由旋转的性质得,∠E′AC=∠F′AB,AE′=AF′,
在△CAE′和△BAF′中,
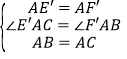 ,
,
∴△CAE′≌△BAF′(SAS),
∴CE′=BF′=6;
②由(1)可知AE=BC,
所以,在△AEF绕点A逆时针旋转过程中,点E经过的路径(圆弧)与过点C且与AB平行的直线l相交于点M、N,如图,
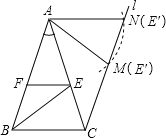
①当点E的像E′与点M重合时,四边形ABCM是等腰梯形,
所以,∠BAM=∠ABC=72°,
又∵∠BAC=36°,
∴α=∠CAM=36°;
②当点E的像E′与点N重合时,
∵CE′∥AB,
∴∠AMN=∠BAM=72°,
∵AM=AN,
∴∠ANM=∠AMN=72°,
∴∠MAN=180°72°×2=36°,
∴α=∠CAN=∠CAM+∠MAN=36°+36°=72°,
综上所述,当旋转角α为36°或72°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
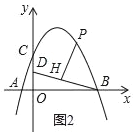
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+4交x轴于点A(﹣2,0)和B(B在A右侧),交y轴于点C,直线y=![]() 经过点B,交y轴于点D,且D为OC中点.
经过点B,交y轴于点D,且D为OC中点.
(1)求抛物线的解析式;
(2)若P是第一象限抛物线上的一点,过P点作PH⊥BD于H,设P点的横坐标是t,线段PH的长度是d,求d与t的函数关系式;
(3)在(2)的条件下,当d=![]() 时,将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q,求点Q的坐标.
时,将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】单位为了解3500名党员职工每月党费上交情况,从中随机抽取50名党员职工,根据每月每名党员职工的党费情况给制如图所示的条形统计图.
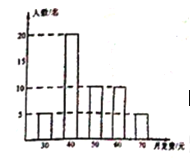
(1)求50名党职工每月觉费的平均数;
(2)直接写出这50名党员职工每月党费的众数与中位数;
(3)根据这50名党员职工每月党费的平均数,请你估计该单位3500名党员职工每月约上交党费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,动点P在射线CB上(与B、C不重合),连结AP,过D作DF∥AP交直线BC于点F,过F作FE⊥直线BD于点E,连结AE、PE.
(1)如图,当点P在线段CB上时
①求证:△ABP≌△DCF;
②点P在运动过程中,探究:△AEP的形状是否发生变化,若不变,请判断△AEP的形状,并说明理由;
(2)如图,当点P在CB的延长线上时,若正方形ABCD的边长为1,设BP=x,当x为何值时,DF平分∠BDC?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠C=30°,AC=48,点D从点C出发沿CA方向以每秒4个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒2个单位长的速度向点B匀速运动,当其中一个点到达终点,另一个点也随之停止运动,设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.当四边形BFDE是矩形时,t的值是______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蕲春新长途客运站准备在七一前建成营运,后期工程若请甲乙两个工程队同时施工,8 天可以完工, 需付两工程队施工费用 7040 元;若先请甲工程队单独施工 6 天,再请乙工程队单独施工 12 天可以完 工,需付两工程队施工费用 6960 元。
(1)甲、乙两工程队施工一天,应各付施工费用多少元?
(2)若想付费用较少,选择哪个工程队?若想尽早完工,选择哪个工程队?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以线段
,以线段![]() 为边向外作等边
为边向外作等边![]() ,点
,点![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() 并延长交线段
并延长交线段![]() 于点
于点![]() .
.
(1)求证:四边形![]() 为平行四边形;
为平行四边形;
(2)求平行四边形![]() 的面积;
的面积;
(3)如图,分别作射线![]() ,
,![]() ,如图中
,如图中![]() 的两个顶点
的两个顶点![]() ,
,![]() 分别在射线
分别在射线![]() ,
,![]() 上滑动,在这个变化的过程中,求出线段
上滑动,在这个变化的过程中,求出线段![]() 的最大长度.
的最大长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
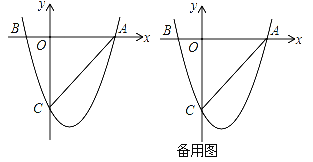
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣3)
(1)求该二次函数的解析式;
(2)设E是y轴右侧抛物线上异于点A的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH,则在点E的运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)设P点是x轴下方的抛物线上的一个动点,连接PA、PC,求△PAC面积的取值范围,若△PAC面积为整数时,这样的△PAC有几个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地现有绿地9万公顷,由于植被遭到严重破坏,土地沙化速度竟达到每年0.3万公顷,照此速度发展下去,设t年后该地剩余绿地面积为S万公顷.
(1)求剩余绿地面积S与t的函数表达式,并写出自变量的取值范围;
(2)画出此函数的图象;
(3)若当剩余绿地面积为0.9万公顷时达到红色警戒线,请计算几 年后该地的绿地面积达到红色警戒线?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com