
����Ŀ��ޭ���³�;����վ������һǰ����Ӫ�ˣ����ڹ�����������������̶�ͬʱʩ����8 ������깤�� �踶�����̶�ʩ������ 7040 Ԫ����������̶ӵ���ʩ�� 6 �죬�����ҹ��̶ӵ���ʩ�� 12 ������� �����踶�����̶�ʩ������ 6960 Ԫ��
��1���ס��������̶�ʩ��һ�죬Ӧ����ʩ�����ö���Ԫ��
��2�����븶���ý��٣�ѡ���ĸ����̶ӣ����뾡���깤��ѡ���ĸ����̶ӣ�
���𰸡���1�����̶�ÿ�������600Ԫ���ҹ��̶�ÿ�������280Ԫ����2����ʱ��������ѡ���̶ӣ��ӷ���������ѡ�ҹ��̶ӣ�
��������
��1������̶�ÿ�������xԪ���ҹ��̶�ÿ�������yԪ����������ɵã����Һ���8���깤���踶�����̶�ʩ������7040Ԫ���ӵ���ʩ��6�죬�����ҹ��̶ӵ���ʩ��12���깤���踶�����̶�ʩ������6960Ԫ���з�������⣮
��2������̶�ÿ����ɵĹ�����Ϊa�ҹ��̶�ÿ����ɵĹ�����Ϊb����ɵ�8a+8b=1��6a+12b=1����֮�ɵü��������̶ӵĹ�������Ч�ʣ���֪�Ǹ��ɵÿ죬�����ɵõ����������̶ӷ��ã�
�⣺����̶�ÿ�������xԪ���ҹ��̶�ÿ�������yԪ��
������ã�![]() ��
��
��ã�![]() ��
��
�𣺼��̶�ÿ�������600Ԫ���ҹ��̶�ÿ�������280Ԫ��
��2������̶�ÿ����ɵĹ�����Ϊa���ҹ��̶�ÿ����ɵĹ�����Ϊb���������
![]() ��
��
��ã�
 ��
��
���̶�Ҫ12����ɣ��ҹ��̶�Ҫ24����ɣ�
���̶ӷ���Ϊ��12��600=7200��Ԫ�����ҹ��̶ӷ���Ϊ��24��280=6720��Ԫ��
��ʱ��������ѡ���̶ӣ��ӷ���������ѡ�ҹ��̶ӣ�


 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���EΪCD��һ�㣬����BCE��BE���ۺ��Cǡ������AD���ϵĵ�F������F��FH��BC��H����BE��G������CG��
��1����֤���ı���CEFG�����Σ�
��2����AB=8��BC=10�����ı���CEFG�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��k1x��b��˫����y��![]() �ཻ��A(1,2)��B(m����1)������
�ཻ��A(1,2)��B(m����1)������
(1)��ֱ�ߺ�˫���ߵĽ���ʽ��
(2)��A1(x1��y1)��A2(x2��y2)��A3(x3��y3)Ϊ˫�����ϵ���������x1��x2��0��x3����ֱ��д��y1��y2��y3�Ĵ�С��ϵʽ��
(3)�۲�ͼ������ֱ��д������ʽk1x��b��![]() �Ľ⼯��
�Ľ⼯��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�EΪCD��һ�㣬FΪBC���ӳ�����һ�㣬��CE=CF.BE��DF֮���������Ĺ�ϵ����˵������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
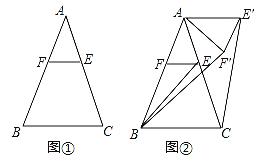
����Ŀ����֪����ABC����AB=AC����E�DZ�AC��һ��������E��EF��BC��AB�ڵ�F
��1����ͼ�٣���֤��AE=AF��
��2����ͼ�ڣ�����AEF�Ƶ�A��ʱ����ת����0�㣼����144�㣩�õ���AE��F��������CE��BF�䣮
����BF��=6����CE���ij���
������EBC=��BAC=36�㣬��ͼ������ת����������CE���ABʱ��ֱ��д����ת�����Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�����BD����BD��CD������A��AM��BD�ڵ�M������D��DN��AB�ڵ�N����DN��![]() ����DB���ӳ�����ȡһ��P�������ABD����MAP����PAB����AP��_____.
����DB���ӳ�����ȡһ��P�������ABD����MAP����PAB����AP��_____.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Դ�����������ܣ�Խ��Խ�ܵ������ߵ�ϲ��.����Ʒ�����Ͷ���г�.һ��ó��˾����ijƷ������Դ����.ȥ�������ܶ�Ϊ5000��Ԫ������1~5�·ݣ�ÿ���������ۼ۸��ȥ�꽵��1��Ԫ.����������ȥ��һ�������ͬ.�����ܶ��ȥ��һ�������20%������1~5�·�ÿ���������ۼ۸��Ƕ�����Ԫ?�����1~5�·�ÿ���������ۼ۸�Ϊx��Ԫ.�������⣬�з�����ȷ����( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
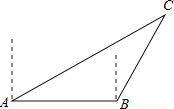
����Ŀ��������һ����C��������Χ12�����а������洬������Ⱥ��������![]() ��A����õ���C�ڱ�ƫ��60�㣬����20�����B�㣬��ʱ��õ���C�ڱ�ƫ��30�㣬����洬���ı亽�������У���û�д�����Σ�գ�
��A����õ���C�ڱ�ƫ��60�㣬����20�����B�㣬��ʱ��õ���C�ڱ�ƫ��30�㣬����洬���ı亽�������У���û�д�����Σ�գ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڽ����ѧ����Ĺ����У����dz��õ����������ۡ�����ѧ˼�룬���������÷������۵���ѧ˼��������Ĺ��̣�����ϸ�Ķ����������Ŀ������ġ�̽����
��������⣩����������a��b��c����abc��0����![]() ��ֵ��
��ֵ��
��������⣩
�⣺������ã�a��b��c������������Ϊ����������һ��Ϊ������������Ϊ������
��a��b��c������������a��0��b��0��c��0ʱ��
��![]() =
=![]() =1+1+3��
=1+1+3��
�ڵ�a��b��c��һ��Ϊ������������Ϊ����ʱ����a��0��b��0��c��0��
��![]() =
=![]() =1+����1��+����1��=��1
=1+����1��+����1��=��1
����![]() ��ֵΪ3��1��
��ֵΪ3��1��
��̽�������������Ľ���˼·�����������⣺
��1������������a��b��c����abc��0����![]() ��ֵ��
��ֵ��
��2����֪|a|=3��|b|=1����a��b����a+b��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com