
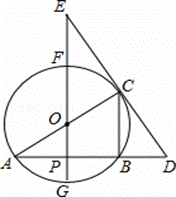
如图,⊙O中,FG、AC是直径,AB是弦,FG⊥AB,垂足为点P,过点C的直线交AB的延长线于点D,交GF的延长线于点E,已知AB=4,⊙O的半径为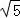 .
.
(1)分别求出线段AP、CB的长;
(2)如果OE=5,求证:DE是⊙O的切线;
(3)如果tan∠E= ,求DC的长
,求DC的长
. 
解答:
(1)解:∵AC为直径,
∴∠ABC=90°,
在Rt△ABC中,AC=2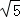 ,AB=4,
,AB=4,
∴BC=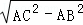 =2,--------------2分
=2,--------------2分
∵直径FG⊥AB,
∴AP=BP=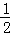 AB=2;--------------3分
AB=2;--------------3分
(2)证明:∵AP=BP,
∴OP为△ABC的中位线,
∴OP=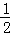 BC=1,
BC=1,
∴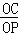 =
= ,
,
而 =
= =
=
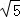 ,
,
∴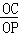 =
=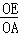 ,--------------5分
,--------------5分
∵∠EOC=∠AOP,
∴△EOC∽△AOP,--------------6分
∴∠OCE=∠OPA=90°,
∴OC⊥DE,
∴DE是⊙O的切线;--------------7分
(3)解:∵BC∥EP,
∴∠DCB=∠E,
∴tan∠DCB=tan∠E=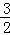
在Rt△BCD中,BC=2,tan∠DCB=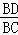 =
=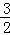 ,
,
∴BD=3,-------------9分
∴CD=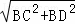 =
= ,--------------10分
,--------------10分


科目:初中数学 来源: 题型:
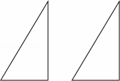
如图是两个全等的含30°角的直角三角形.
(1)将其相等边拼在一起,组成一个没有重叠部分的平面图形,请你画出所有不同的拼接平面图形的示意图;
(2)若将(1)中平面图形分别印制在质地、形状、大小完全相同的卡片上,洗匀后从中随机抽取一张,求抽取的卡片上平面图形为轴对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
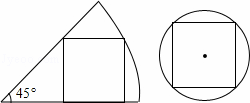
一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是--------( )
|
| A. | 5:4 | B. | 5:2 | C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C,D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为 .
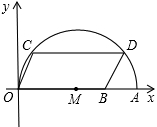
查看答案和解析>>
科目:初中数学 来源: 题型:
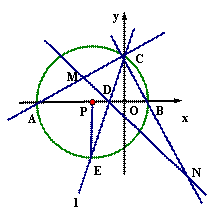
在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的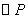 过点C,若C的坐标为(0,2),AB=5, 经过A、B、C三点的抛物线为y=ax2+bx+c。
过点C,若C的坐标为(0,2),AB=5, 经过A、B、C三点的抛物线为y=ax2+bx+c。
(1)求点A、B的坐标及抛物线的解析式。
(2)若∠ACB的平分线所在的直线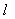 交x轴于点D,交圆于点E。
交x轴于点D,交圆于点E。
①求证:PE⊥x轴;
②试求直线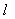 对应的一次函数的解析式.
对应的一次函数的解析式.
(3)过点D任作一直线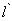 分别交射线CA,CB(点C除外)于点M,N,则
分别交射线CA,CB(点C除外)于点M,N,则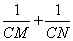 的值是否为定值,若是,求出定值,若不是,请说明理由
的值是否为定值,若是,求出定值,若不是,请说明理由
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com