
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )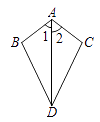
A.AB=AC
B.BD=CD
C.∠B=∠C
D.∠BDA=∠CDA
【答案】B
【解析】解:A、∵∠1=∠2,AD为公共边,若AB=AC,则△ABD≌△ACD(SAS);故A不符合题意;
B、∵∠1=∠2,AD为公共边,若BD=CD,不符合全等三角形判定定理,不能判定△ABD≌△ACD;故B符合题意;
C、∵∠1=∠2,AD为公共边,若∠B=∠C,则△ABD≌△ACD(AAS);故C不符合题意;
D、∵∠1=∠2,AD为公共边,若∠BDA=∠CDA,则△ABD≌△ACD(ASA);故D不符合题意.
故答案为:B.
由图知,两三角形已经有一个角,及夹这个角的一条边对应相等,需要全等的话,只需加夹这个角的另一条边,或任意一对角相等即可,从而一一判断即可得出结论。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,从下列四个条件:①BC=B′C;②AC=A′C;③∠A′CA=∠B′CB;④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解我校初三年级2000名学生的体重情况,从中抽查了100名学生的体重进行统计分析,在这个问题中,样本是( )
A.2000名学生的体重B.100
C.100名学生D.100名学生的体重
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中;
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;②小明通过观察、实验,提出猜想:在点P,Q运动的过程中,始终有PA=PM,小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证PA=PM,只需证△APM是等边三角形.
想法2:在BA上取一点N,使得BN=BP,要证PA=PM,只需证△ANP≌△PCM.……
请你参考上面的想法,帮助小明证明PA=PM(一种方法即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,DE是AC的垂直平分线.
(1)求证:△BCD是等腰三角形;
(2)△BCD的周长是a,BC=b,求△ACD的周长(用含a,b的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小丽在计算一组数据的方差时,小丽计算的结果为a,小明把其中每个数据都加上2,算出的方差为b,则:( )
A.b=aB.b=2aC.b=a2D.b=4a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ![]() 中,AD是高,E、F分别是AB、AC的中点,
中,AD是高,E、F分别是AB、AC的中点,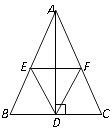
(1)AB=10,AC=8,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系,证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com