
【题目】如图,在 ![]() 中,AD是高,E、F分别是AB、AC的中点,
中,AD是高,E、F分别是AB、AC的中点,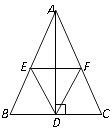
(1)AB=10,AC=8,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系,证明你的结论.
【答案】
(1)解:∵AB=10,AC=8,E、F分别是AB、AC的中点,
∴AE=![]() AB=5,AF=
AB=5,AF=![]() AC=4.
AC=4.
∵AD是高,
∴AD⊥BC.
∵在Rt△ABD和Rt△ADC中,E、F分别是AB、AC的中点,
∴DE=![]() AB=5,DF=
AB=5,DF=![]() AC=4.
AC=4.
∴C四边形AEDF=AE+ED+DF+AF=5+5+4+4=18.
(2)解:EF垂直平分AD,理由如下:
∵由(1)得AE=DE,AF=DF,
∴E、F在AD的垂直平分线上.
∴EF是AD的垂直平分线 ,
∴EF垂直平分AD 。
【解析】(1)根据中点的定义得出;AE,AF的长,根据直角三角形斜边上的中线等于斜边的一半,分别在Rt△ABD和Rt△ADC中求出ED和DF的长,然后根据四边形的周长计算方法算出结果;
(2)由AE=DE,AF=DF,知E、F在AD的垂直平分线上. 根据垂直平分线的判定定理得出结论。


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系![]() 中,
中,![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴及直线
轴及直线![]() 分别交于点
分别交于点![]() ,
,![]() .点
.点![]() ,
,![]() 关于
关于![]() 轴对称,连接
轴对称,连接![]() .
.
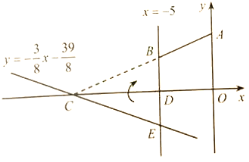
(1)求点![]() ,
,![]() 的坐标及直线
的坐标及直线![]() 的解析式;
的解析式;
(2)设面积的和![]() ,求
,求![]() 的值;
的值;
(3)在求(2)中![]() 时,嘉琪有个想法:“将
时,嘉琪有个想法:“将![]() 沿
沿![]() 轴翻折到
轴翻折到![]() 的位置,而
的位置,而![]() 与四边形
与四边形![]() 拼接后可看成
拼接后可看成![]() ,这样求
,这样求![]() 便转化为直接求
便转化为直接求![]() 的面积不更快捷吗?”但大家经反复验算,发现
的面积不更快捷吗?”但大家经反复验算,发现![]() ,请通过计算解释他的想法错在哪里.
,请通过计算解释他的想法错在哪里.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com