
【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.

【答案】(1)抛物线解析式为y=x2﹣3x﹣4;(2)存在满足条件的P点,其坐标为(![]() ,﹣2)(3)P点坐标为(2,﹣6)时,△PBC的最大面积为8.
,﹣2)(3)P点坐标为(2,﹣6)时,△PBC的最大面积为8.
【解析】
试题分析:(1)由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;(2)由题意可知点P在线段OC的垂直平分线上,则可求得P点纵坐标,代入抛物线解析式可求得P点坐标;(3)过P作PE⊥x轴,交x轴于点E,交直线BC于点F,用P点坐标可表示出PF的长,则可表示出△PBC的面积,利用二次函数的性质可求得△PBC面积的最大值及P点的坐标.
试题解析:(1)设抛物线解析式为y=ax2+bx+c,
把A、B、C三点坐标代入可得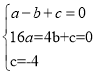 ,解得
,解得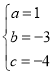 ,
,
∴抛物线解析式为y=x2﹣3x﹣4;
(2)作OC的垂直平分线DP,交OC于点D,交BC下方抛物线于点P,如图1,
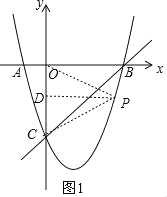
∴PO=PD,此时P点即为满足条件的点,∵C(0,﹣4),∴D(0,﹣2),∴P点纵坐标为﹣2,
代入抛物线解析式可得x2﹣3x﹣4=﹣2,解得x=![]() (小于0,舍去)或x=
(小于0,舍去)或x=![]() ,
,
∴存在满足条件的P点,其坐标为(![]() ,﹣2);
,﹣2);
(3)∵点P在抛物线上,∴可设P(t,t2﹣3t﹣4),
过P作PE⊥x轴于点E,交直线BC于点F,如图2,
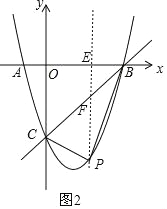
∵B(4,0),C(0,﹣4),∴直线BC解析式为y=x﹣4,∴F(t,t﹣4),
∴PF=(t﹣4)﹣(t2﹣3t﹣4)=﹣t2+4t,
∴S△PBC=S△PFC+S△PFB=![]() PFOE+
PFOE+![]() PFBE=
PFBE=![]() PF(OE+BE)=
PF(OE+BE)=![]() PFOB=
PFOB=![]() (﹣t2+4t)×4=﹣2(t﹣2)2+8,∴当t=2时,S△PBC最大值为8,此时t2﹣3t﹣4=﹣6,
(﹣t2+4t)×4=﹣2(t﹣2)2+8,∴当t=2时,S△PBC最大值为8,此时t2﹣3t﹣4=﹣6,
∴当P点坐标为(2,﹣6)时,△PBC的最大面积为8.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在轴的负半轴、轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y=![]() (x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=
(x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=![]() ,,则BN的长为______________.
,,则BN的长为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中;
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;②小明通过观察、实验,提出猜想:在点P,Q运动的过程中,始终有PA=PM,小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证PA=PM,只需证△APM是等边三角形.
想法2:在BA上取一点N,使得BN=BP,要证PA=PM,只需证△ANP≌△PCM.……
请你参考上面的想法,帮助小明证明PA=PM(一种方法即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小丽在计算一组数据的方差时,小丽计算的结果为a,小明把其中每个数据都加上2,算出的方差为b,则:( )
A.b=aB.b=2aC.b=a2D.b=4a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ![]() 中,AD是高,E、F分别是AB、AC的中点,
中,AD是高,E、F分别是AB、AC的中点,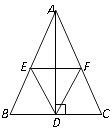
(1)AB=10,AC=8,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某长途汽车客运公司规定旅客可以免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)与行李质量x(kg)之间的函数表达式为 ![]() ,这个函数的图像如图所示,求:
,这个函数的图像如图所示,求:
(1)k和b的值;
(2)旅客最多可免费携带行李的质量;
(3)行李费为4~15元时,旅客携带行李的质量为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,以△ABC 的一边为边画等腰三角形,使得它的第三个顶点在△ABC 的其他边上,试画出所有不同的等腰三角形并说明画图方法.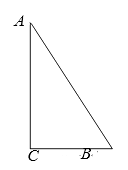
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com