
【题目】如图,在 Rt△ABC 中,以△ABC 的一边为边画等腰三角形,使得它的第三个顶点在△ABC 的其他边上,试画出所有不同的等腰三角形并说明画图方法.
【答案】图示及画法如下:
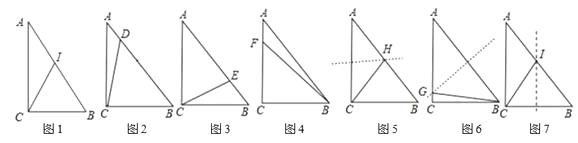
①以 B 为圆心,BC 长为半径画弧,交 AB 于点 I,△BCI 就是等腰三角形;
②以 C 为圆心,BC 长为半径画弧,交 AB 于点 D,△BCD 就是等腰三角形;
③以 A 为圆心,AC 长为半径画弧,交 AB 于点 E,△ACE 就是等腰三角形;
④以 C 为圆心,BC 长为半径画弧,交 AC 于点 F,△BCF 就是等腰三角形;
⑤作 AC 的垂直平分线交 AB 于点 H,△ACH 就是等腰三角形;
⑥作 AB 的垂直平分线交 AC 于 G,则△AGB 是等腰三角形;
⑦作 BC 的垂直平分线交 AB 于 I,则△BCI 是等腰三角形.
【解析】①以 B 为圆心,BC 长为半径画弧,交 AB 于点 I,△BCI 就是等腰三角形;
②以 C 为圆心,BC 长为半径画弧,交 AB 于点 D,△BCD 就是等腰三角形;
③以 A 为圆心,AC 长为半径画弧,交 AB 于点 E,△ACE 就是等腰三角形;
④以 C 为圆心,BC 长为半径画弧,交 AC 于点 F,△BCF 就是等腰三角形;
⑤作 AC 的垂直平分线交 AB 于点 H,△ACH 就是等腰三角形;
⑥作 AB 的垂直平分线交 AC 于 G,则△AGB 是等腰三角形;
⑦作 BC 的垂直平分线交 AB 于 I,则△BCI 是等腰三角形.
【考点精析】关于本题考查的等腰三角形的判定,需要了解如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 为
为![]() 中点,点
中点,点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() ,
,![]() 重合),将
重合),将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到扇形
后得到扇形![]() ,
,![]() ,
,![]() 分别切优弧
分别切优弧![]() 于点
于点![]() ,
,![]() ,且点
,且点![]() ,
,![]() 在
在![]() 异侧,连接
异侧,连接![]() .
.

(1)求证:![]() ;
;
(2)当![]() 时,求
时,求![]() 的长(结果保留
的长(结果保留![]() );
);
(3)若![]() 的外心在扇形
的外心在扇形![]() 的内部,求
的内部,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】编号为![]() 号的5名学生进行定点投篮,规定每人投5次,每命中1次记1分,没有命中记0分.如图是根据他们各自的累积得分绘制的条形统计图,之后来了第6号学生也按同样记分规定投了5次,其命中率为
号的5名学生进行定点投篮,规定每人投5次,每命中1次记1分,没有命中记0分.如图是根据他们各自的累积得分绘制的条形统计图,之后来了第6号学生也按同样记分规定投了5次,其命中率为![]() .
.
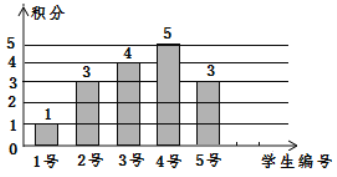
(1)求第6号学生的积分,并将图增补为这6名学生积分的条形统计图;
(2)在这6名学生中,随机选一名学生,求选上命中率高于![]() 的学生的概率;
的学生的概率;
(3)最后,又来了第7号学生,也按同样记分规定投了5次.这时7名学生积分的众数仍是前6名学生积分的众数,求这个众数,以及第7号学生的积分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:①图中全等的三角形只有两对;②△ABC的面积等于四边形CDOE面积的2倍;③OD=OE;④CE+CD=BC,其中正确的结论有( )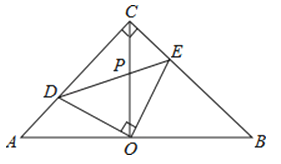
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具经销店在开学时购进了A、B两种型号的计算器,已知:购进A型号的计算器20个,B型号的计算器25个需用1265元;购进A型号的计算器16个,B型号的计算器12个需用748元.求:
(1)A、B两种型号的计算器进价分别是多少元?
(2)在(1)的条件下,若A型号的计算器的售价是30元/个,B型号的计算器的售价是45元/个,商店一次性购进两种型号的计算器各20个,并全部销售,求商店所获利润是多少元?
(3)在两种型号计算器的进价和售价均保持不变的情况下,该商店准备购进A、B两种型号的计算器共40个,且A型号的计算器的数量不得少于5个,问:商店应怎样进货,才能使所获利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com