
【题目】如图,![]() ,
,![]() 为
为![]() 中点,点
中点,点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() ,
,![]() 重合),将
重合),将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到扇形
后得到扇形![]() ,
,![]() ,
,![]() 分别切优弧
分别切优弧![]() 于点
于点![]() ,
,![]() ,且点
,且点![]() ,
,![]() 在
在![]() 异侧,连接
异侧,连接![]() .
.

(1)求证:![]() ;
;
(2)当![]() 时,求
时,求![]() 的长(结果保留
的长(结果保留![]() );
);
(3)若![]() 的外心在扇形
的外心在扇形![]() 的内部,求
的内部,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() ;(3)4<OC<8.
;(3)4<OC<8.
【解析】(1)连接OQ,证明AP,BQ所在两个三角形全等;(2)在Rt△BOQ中,由OB,BQ的长求出∠BOQ的度数,得到![]() 所对圆心角的度数,再根据弧长公式求解;(3)△APO的外心是OA的中点,
所对圆心角的度数,再根据弧长公式求解;(3)△APO的外心是OA的中点,
试题分析:
试题解析:(1)证明:连接OQ.
∵AP,BQ分别与![]() 相切,∴OP⊥AP,OQ⊥BQ,即∠P=∠Q=90°.
相切,∴OP⊥AP,OQ⊥BQ,即∠P=∠Q=90°.
∵OA=OB,OP=OQ,∴Rt△APO≌Rt△BQO.∴AP=BQ.
(2)∵BQ=![]() ,OB=
,OB=![]() =8,∠Q=90°,∴sin∠BOQ=
=8,∠Q=90°,∴sin∠BOQ=![]() ,∴∠BOQ=60°.
,∴∠BOQ=60°.
∵OQ=8×cos60°=4,∴![]() 的长为
的长为![]() =
=![]() .
.
(3)设点M为Rt△APO的外心,则M为OA的中点,∴OM=4.
当点M在扇形的内部时,OM<OC,∴4<OC<8.
![]()



科目:初中数学 来源: 题型:
【题目】在等边△ABC中;
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;②小明通过观察、实验,提出猜想:在点P,Q运动的过程中,始终有PA=PM,小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证PA=PM,只需证△APM是等边三角形.
想法2:在BA上取一点N,使得BN=BP,要证PA=PM,只需证△ANP≌△PCM.……
请你参考上面的想法,帮助小明证明PA=PM(一种方法即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某长途汽车客运公司规定旅客可以免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)与行李质量x(kg)之间的函数表达式为 ![]() ,这个函数的图像如图所示,求:
,这个函数的图像如图所示,求:
(1)k和b的值;
(2)旅客最多可免费携带行李的质量;
(3)行李费为4~15元时,旅客携带行李的质量为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,以△ABC 的一边为边画等腰三角形,使得它的第三个顶点在△ABC 的其他边上,试画出所有不同的等腰三角形并说明画图方法.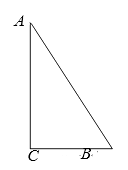
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查适合采用抽样调查的是( )
A.检查一枚用于发射卫星的运载火箭的各零部件
B.了解全班同学身高状况
C.检查一批灯泡的使用寿命
D.奥运会上对参赛运动员进行的尿样检查
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com