
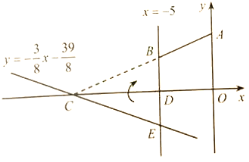
【题目】如图,直角坐标系![]() 中,
中,![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴及直线
轴及直线![]() 分别交于点
分别交于点![]() ,
,![]() .点
.点![]() ,
,![]() 关于
关于![]() 轴对称,连接
轴对称,连接![]() .
.
(1)求点![]() ,
,![]() 的坐标及直线
的坐标及直线![]() 的解析式;
的解析式;
(2)设面积的和![]() ,求
,求![]() 的值;
的值;
(3)在求(2)中![]() 时,嘉琪有个想法:“将
时,嘉琪有个想法:“将![]() 沿
沿![]() 轴翻折到
轴翻折到![]() 的位置,而
的位置,而![]() 与四边形
与四边形![]() 拼接后可看成
拼接后可看成![]() ,这样求
,这样求![]() 便转化为直接求
便转化为直接求![]() 的面积不更快捷吗?”但大家经反复验算,发现
的面积不更快捷吗?”但大家经反复验算,发现![]() ,请通过计算解释他的想法错在哪里.
,请通过计算解释他的想法错在哪里.
【答案】(1)C(-13,0),E(-5,-3),![]() ;(2)32;(3)见解析.
;(2)32;(3)见解析.
【解析】
试题分析:(1)由![]() 与x轴和直线x=-5的交点求得点C,E的坐标,点B,E关于x轴对称,求得B的坐标,由待定系数法求直线AB的解析式;(2)分别求△CDE的面积和梯形ABDO的面积;(3)点C不在直线AB上.
与x轴和直线x=-5的交点求得点C,E的坐标,点B,E关于x轴对称,求得B的坐标,由待定系数法求直线AB的解析式;(2)分别求△CDE的面积和梯形ABDO的面积;(3)点C不在直线AB上.
试题解析:(1)把y=0代入![]() ,解得x=-13,∴C(-13,0).
,解得x=-13,∴C(-13,0).
把x=-5代入![]() ,解得y=-3,∴E(-5,-3).
,解得y=-3,∴E(-5,-3).
∵点B,E关于x轴对称,∴B(-5,3).
设直线AB的解析式为y=kx+b,则![]() 解得
解得![]()
∴直线AB的解析式为![]() .
.
(2)∵CD=8,DE=DB=3,OA=OD=5,
∴![]() ,
,![]() ,即S=32.
,即S=32.
(3)当x=-13时,![]() =-0.2≠0.
=-0.2≠0.
∴点C不在直线AB上,即A,B,C三点不共线.
∴他的想法错在将△CDB与四边形ABDO拼接后看成了△AOC.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】为了了解我校初三年级2000名学生的体重情况,从中抽查了100名学生的体重进行统计分析,在这个问题中,样本是( )
A.2000名学生的体重B.100
C.100名学生D.100名学生的体重
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ![]() 中,AD是高,E、F分别是AB、AC的中点,
中,AD是高,E、F分别是AB、AC的中点,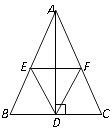
(1)AB=10,AC=8,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中属于不确定事件的是( )
A.抛出的篮球会落下B.从装有黑球,白球的袋里摸出红球
C.367人中至少有2人是同月同日出生D.买1张彩票,中500万大奖
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com