
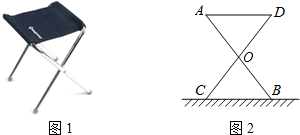
分析 根据中点定义求出OA=OB,OC=OD,然后利用“边角边”证明△AOD和△BOC全等,根据全等三角形对应边相等即可证明.
解答 解:∵O是AB、CD的中点,
∴OA=OB,OC=OD,
在△AOD和△BOC中,$\left\{\begin{array}{l}{OA=OB}\\{∠AOD=∠BOC}\\{OC=OD}\end{array}\right.$,
∴△AOD≌△BOC(SAS),
∴CB=AD,
∵AD=30cm,
∴CB=30cm.
所以,依据是两边及夹角对应相等的两个三角形全等,全等三角形对应边相等.
故答案为:两边及夹角对应相等的两个三角形全等,全等三角形对应边相等.
点评 本题考查了全等三角形的应用,比较简单,证明得到三角形全等是解题的关键.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
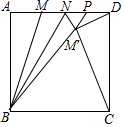 如图,正方形ABCD的边长为6,AM=$\frac{1}{3}$AD,点N在线段MD上,连接BN,把△BMN沿BN翻折,得到△BM′N,延长BM′交线段DN于点P,连接CM′,DM′,当△CDM′是等腰三角形时,MN的长为$\frac{131-24\sqrt{65}}{8}$或=$\frac{19\sqrt{31}+16}{54}$.
如图,正方形ABCD的边长为6,AM=$\frac{1}{3}$AD,点N在线段MD上,连接BN,把△BMN沿BN翻折,得到△BM′N,延长BM′交线段DN于点P,连接CM′,DM′,当△CDM′是等腰三角形时,MN的长为$\frac{131-24\sqrt{65}}{8}$或=$\frac{19\sqrt{31}+16}{54}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com