
 如图,AB是⊙O的直径,$\widehat{ED}$=$\widehat{BD}$,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.交AM于点N,且OA=CD=$\sqrt{2}$.
如图,AB是⊙O的直径,$\widehat{ED}$=$\widehat{BD}$,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.交AM于点N,且OA=CD=$\sqrt{2}$.分析 (1)连接OD,通过证明OD∥AM,得到∠M=∠ODB,因为OD=OB,所以∠ODB=∠ABM,所以∠M=∠OBD,根据等腰三角形的判定得到AM=AB;
(2)同切线的性质,得到OD⊥CD,从而证得△OCD为等腰直角三角形,得到∠DOC=45°,根据S阴影=S△OCD-S扇OBD计算即可得解;
(3)连接AD,因为CD是⊙O的切线,根据切线长定理得,CD2=CB•CA,从而求得AC的长,在等腰Rt△ANC中,根据勾股定理可求得AN的长.
解答 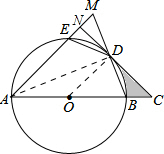 解:(1)证明:如图,连接OD,
解:(1)证明:如图,连接OD,
∵$\widehat{ED}$=$\widehat{BD}$,
∴∠MAD=∠DAB,
∵OA=OD,
∴∠DAB=∠ODA,
∴∠MAD=∠DAB=∠ODA,
∵∠DOC=∠DAB+∠ODA=2∠DAB,
而∠MAB=2∠DAB,
∴∠MAB=∠DOC,
∴OD∥AM,
∴∠M=∠ODB,
∵OD=OB,
∴∠BDO=∠OBD,
∴∠M=∠OBD,
∴AB=AM,
(2)解:∵CD是⊙O切线,
∴OD⊥CD,
∵OA=CD=$\sqrt{2}$,OA=OD,
∴OD=CD=$\sqrt{2}$,
∴△OCD为等腰直角三角形,
∴∠DOC=∠C=45°,
∴S阴影=S△OCD-S扇OBD=$\frac{1}{2}×\sqrt{2}×\sqrt{2}-\frac{45π×(\sqrt{2})^{2}}{360}$=$1-\frac{π}{4}$
(3)解: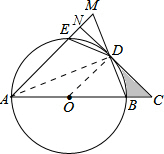 连结AD,
连结AD,
∵DC是⊙O的切线,
∴DC2=CB•CA=(CA-AB)•CA,
∴($\sqrt{2}$)2=(CA-2$\sqrt{2}$)•CA,
解,得CA=2+$\sqrt{2}$,
在Rt△ANC中,∠ANC=90°,AN=NC,
∵AN2+CN2=AC2,
∴AN=$\frac{\sqrt{2}}{2}$AC=$\frac{\sqrt{2}}{2}$(2+$\sqrt{2}$)=$\sqrt{2}$+1.
点评 本题考查的是切线的性质、弦、弧之间的关系、扇形面积的计算,掌握切线的性质定理和扇形的面积公式是解题的关键,注意辅助线的作法.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 无理数与无理数的和一定是无理数 | B. | 有理数与无理数的和一定是无理数 | ||
| C. | 有理数乘无理数的积一定是无理数 | D. | 无理数乘无理数的积一定是无理数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,边长为a的正方形ABCD中,E,F是边AD,AB上两点(与端点不重合),且AE=BF,连接CE,DF相交于点M.
如图,边长为a的正方形ABCD中,E,F是边AD,AB上两点(与端点不重合),且AE=BF,连接CE,DF相交于点M.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 项目 | 着装 | 队形 | 精神风貌 |
| 成绩(分) | 90 | 94 | 92 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 点P是等腰直角三角形ABC底边BC上一点,过点P作BA、AC的垂线,垂足为E、F,设D为BC的中点.
点P是等腰直角三角形ABC底边BC上一点,过点P作BA、AC的垂线,垂足为E、F,设D为BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 2015年12月,某市总工会组织该市各单位参加“迎新春长跑活动”,组委会将男动员分成三组:老年组、中年组和青年组,根据报名情况,制作了如图所示的人数扇形统计图,已知青年人组共有210人,则老年组共有30人.
2015年12月,某市总工会组织该市各单位参加“迎新春长跑活动”,组委会将男动员分成三组:老年组、中年组和青年组,根据报名情况,制作了如图所示的人数扇形统计图,已知青年人组共有210人,则老年组共有30人.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com