练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知三角形三边分别为2，a-1，4，那么a的取值范围是（　　）

    A. 1＜a＜5B. 2＜a＜6C. 3＜a＜7D. 4＜a＜6

    【答案】C

    【解析】

    本题可根据三角形的三边关系：两边之和大于第三边，两边之差小于第三边列出不等式：4-2＜a-1＜4+2，化简即可得出a的取值范围．

    解：依题意得：4-2＜a-1＜4+2，
    即：2＜a-1＜6，
    ∴3＜a＜7．
    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下面是某同学对多项式（x2－4x-3）（x2－4x+1）+4进行因式分解的过程．

    解：设x2－4x=y

    原式=（y-3）（y+1）+4 （第一步）

    = y2-2y+1 （第二步）

    =（y-1）2 （第三步）

    =（x2－4x-1）2 （第四步）

    回答下列问题：

    （1）该同学第二步到第三步运用了因式分解的_______．

    A．提取公因式法 B．平方差公式法 C.完全平方公式法

    （2）请你模仿以上方法尝试对多项式（x2+2x）（x2+2x+2）+1进行因式分解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】芝麻作为食品和药物，均广泛使用．经测算，一粒芝麻约有0.00000201千克，用科学记数法表示为（ ）
    A.2.01×10﹣6千克
    B.0.201×10﹣5千克
    C.20.1×10﹣7千克
    D.2.01×10﹣7千克

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先化简再求值：(2x＋3)(2x－3)－4x(x－1)－(x－2)2，其中x＝2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明在学习三角形内角和定理时，自己做了如下推理过程，请你帮他补充完整．

    已知：如图，△ABC中，∠A、∠B、∠C是它的三个内角，那么这三个内角的和等于多少？为什么？

    解：∠A+∠B+∠C=180°

    理由：作∠ACD=∠A，并延长BC到E

    ∠1=∠A（已作）

    ∴AB∥CD （_________________________）

    ∴∠B=_____（_________________________）

    而∠ACB+∠1+∠2=180°

    ∴∠ACB+_____+_____=180°（等量代换）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，已知直线AB的函数解析式为y=﹣2x+8，与x轴交于点A，与y轴交于点B．

    （1）求A、B两点的坐标；

    （2）若点P（m，n）为线段AB上的一个动点（与A、B不重合），作PE⊥x轴于点E，PF⊥y轴于点F，连接EF，问：

    ①若△PAO的面积为S，求S关于m的函数关系式，并写出m的取值范围；

    ②是否存在点P，使EF的值最小？若存在，求出EF的最小值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列四个数中，最小的是（ ）
    A.0
    B.﹣2
    C.﹣8
    D.1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“x与5的差不小于x的2倍”用不等式表示为________________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

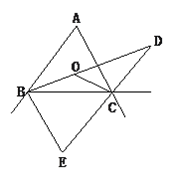
    【题目】如图所示,∠ABC,∠ACB的内角平分线交于点O,∠ABC 的内角平分线与∠ACB的外角平分线交于点D,∠ABC与∠ACB的相邻外角平分线交于点E,且∠A=60°, 则∠BOC=_______,∠D=_____,∠E=________.

    查看答案和解析>>

    同步练习册答案