
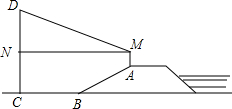
 如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:$\sqrt{3}$,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30$\sqrt{3}$m.
如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:$\sqrt{3}$,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30$\sqrt{3}$m.分析 (1)延长MA交直线BC于点E,在直角△ABE中由i的值即可求得堤坝的高AE;
(2)解直角△ABE,求出BE的长,从而求得MN的长度,再解直角△DMN,求得DN的高度,那么CD=DN+NC=DN+MA+AE,代入数据计算即可.
解答 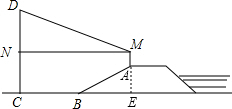 解:(1)延长MA交直线BC于点E,
解:(1)延长MA交直线BC于点E,
∵在直角△ABE中,AB=30m,i=1:$\sqrt{3}$,
∴AE=15m,BE=15$\sqrt{3}$m;
(2)MN=BC+BE=30$\sqrt{3}$+15$\sqrt{3}$=45$\sqrt{3}$,
∵在直角△DMN中,∠NMD=30°,
∴DN=MN•tan30°=45$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=45,
∴CD=DN+NC=DN+MA+AE=45+1.5+15=61.5(m).
点评 本题考查了解直角三角形的应用-坡度坡角问题,由i的值求得堤坝的高AE和BE,求得MN,由仰角求得DN高度,进而求得总高度.


科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{1-x}{\sqrt{3x-1}}$ | B. | y=$\sqrt{\frac{1-x}{3x-1}}$ | C. | y=$\frac{\sqrt{3x-1}}{1-x}$ | D. | y=$\frac{1}{\sqrt{1-x}}$-$\sqrt{3x-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,?ABC是⊙O的内接三角形,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连接AD.
如图,?ABC是⊙O的内接三角形,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
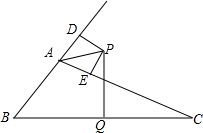 如图,△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB于D,PE⊥AC于E.
如图,△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB于D,PE⊥AC于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
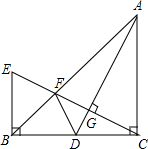 如图,在△ABC中,∠BCA=90°,CA=CB,AD为BC边上的中线,CG⊥AD于G,交AB于F,过点B作BC的垂线交CG于E.求证:∠ADC=∠BDF.
如图,在△ABC中,∠BCA=90°,CA=CB,AD为BC边上的中线,CG⊥AD于G,交AB于F,过点B作BC的垂线交CG于E.求证:∠ADC=∠BDF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
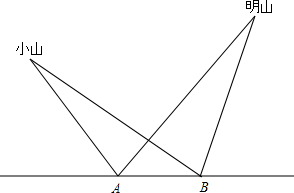 九年级学生小明的家乡有用平直的公路连接起来的小山和明山,如图所示,小明在A处测得小山和明山的顶峰仰角均为45°.他又从A处沿公路向明山前进100m到达B处,测得小山和明山的仰角分别为30°和60°,求小山和明山的高度.(计算结果精确到1m,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
九年级学生小明的家乡有用平直的公路连接起来的小山和明山,如图所示,小明在A处测得小山和明山的顶峰仰角均为45°.他又从A处沿公路向明山前进100m到达B处,测得小山和明山的仰角分别为30°和60°,求小山和明山的高度.(计算结果精确到1m,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com