
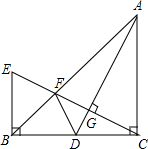
 如图,在△ABC中,∠BCA=90°,CA=CB,AD为BC边上的中线,CG⊥AD于G,交AB于F,过点B作BC的垂线交CG于E.求证:∠ADC=∠BDF.
如图,在△ABC中,∠BCA=90°,CA=CB,AD为BC边上的中线,CG⊥AD于G,交AB于F,过点B作BC的垂线交CG于E.求证:∠ADC=∠BDF. 分析 由条件可知∠ECD+∠ADC=∠E+∠ECD=90°,可得到∠E=∠ADC,再结合条件可证明△ADC≌△CEB,得到BE=CD=BD,结合条件可证明△BEF≌△BDF,则有∠E=∠BDF=∠ADC,可得结论.
解答 证明:∵∠BCA=90°,
∴∠DCG+∠GCA=90°,
∵CG⊥AD,
∴∠GCA+∠CAG=90°,
∴∠DCG=∠CAG,
在△EBC和△DCA中,
$\left\{\begin{array}{l}{∠EBC=∠DCA}\\{BC=AC}\\{∠DCG=∠CAG}\end{array}\right.$,
∴△ADC≌△CEB(ASA),
∴BE=DC,∠E=∠ADC,
∵∠EBC=90°,∠ABC=45°,
∴∠EBF=∠DBF=45°,
∵BD=DC,
∴BE=BD,
在△EBF和△DBF中,
$\left\{\begin{array}{l}{BE=BD}\\{∠EBF=∠DBF}\\{BF=BF}\end{array}\right.$,
∴△EBF≌△DBF(SAS),
∴∠E=∠BDF,
∴∠ADC=∠BDF.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法SSS、SAS、ASA、AAS和HL是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=12cm,BC=15cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以2cm/s的速度向B点运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,使PQ=CD,需经过多少时间?为什么?
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=12cm,BC=15cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以2cm/s的速度向B点运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,使PQ=CD,需经过多少时间?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 1 | 2 | 3 | 4 | 5 |
| 用水量(吨) | 8 | 10 | 13 | 15 | 18 |
| 费 用(元) | 16 | 20 | 29 | 35 | 44 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
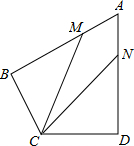 如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则∠BCD=120°,cos∠MCN=$\frac{13}{14}$.
如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则∠BCD=120°,cos∠MCN=$\frac{13}{14}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
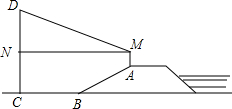 如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:$\sqrt{3}$,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30$\sqrt{3}$m.
如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:$\sqrt{3}$,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30$\sqrt{3}$m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com