
����Ŀ��ijУ���꼶����Ӣ���ݽ�����������1200ԪǮ��ȫ�����꣩����A��B���ֱʼDZ���Ϊ��Ʒ����֪A��B����ÿ���ֱ�Ϊ12Ԫ��20Ԫ���蹺��A��x����B��y����
��1����y����x�ĺ�������ʽ��
��2��������A�ֵ�����������B�ֵ�������
�������ٹ���A�ֶ��ٱ���
�ڸ��ݢٵĹ�����B��̫�࣬�ڷ��ò��������°�һ����B�ֵ�������һ��C��������C�ֵ���������B�ֵ���������֪C��ÿ��8Ԫ���������C��������______����ֱ��д���𰸣�
���𰸡���1��y��![]() ����2�������ٹ���A��40������30��
����2�������ٹ���A��40������30��
��������
��1������A�ֵķ���+B�ֵķ��ã�1200Ԫ������y����x�ĺ�������ʽ��
��2���ٸ��ݹ���A�ֵ�����������B�ֵ��������г�����ʽ������⣻
����B�ֵ�����m����C�ֵ�����n�������������ҳ�m��n�Ĺ�ϵʽ���ٸ��ݵ�����C�ֵ���������B�ֵ��������г�����ʽ������⣮
�⣺��1����12x+20y��1200��
��y��![]() ��
��
��2���١߹���A�ֵ�����������B�ֵ�������
��x��y��
��x��![]() ��
��
��x��![]() ��
��
��x��y��������
�����ٹ���A��40����
����A�ֵ�����Ϊx����B�ֵ�����y����C�ֵ�����c����
��������ã�12x+20y+8c��1200
��y��![]()
��C�ֵ���������B�ֵ�����
��c��y
��c��![]()
��c��![]() ��
��
�߹���A�ֵ�����������B�ֵ�������
��x��y
��x��![]()
��c��150��4x
��c��![]() ��
��
��x��y��c��������
��C��������30��
�ʴ�Ϊ30����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У��ԶԽ���BDΪһ�߹���һ������BDEF��ʹ����һ��EF��ԭ���εĶ���C.
(1)��Rt��CBD�����ΪS1��Rt��BFC�����ΪS2��Rt��DCE�����ΪS3����S1__ __S2��S3��(���������������)
(2)д��ͼ�е��������������Σ���ѡ������һ�Խ���֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��һ�����ڵĵ�A�ڷ���������y��![]() ��ͼ�������ڶ������ڵĵ�B�ڷ���������y��
��ͼ�������ڶ������ڵĵ�B�ڷ���������y��![]() ��ͼ��������OA��OB��cosA��
��ͼ��������OA��OB��cosA��![]() ����k��ֵΪ( )
����k��ֵΪ( )
A. ��3 B. ��4 C. ��![]() D. ��2
D. ��2![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=90������ACB���CAB��ƽ���߽��ڵ�P��PD��AB�ڵ�D������APC����APD���ܳ���Ϊ![]() ���ı���BCPD���ܳ�Ϊ12+
���ı���BCPD���ܳ�Ϊ12+![]() ����BC����______��
����BC����______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
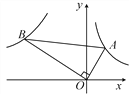
����Ŀ��С���ڰ�����С�׳���ʵ��.��ͼ1���̶���Դ���߶�MN�������Ĺ⾭��С�ף�����K�������߶�M'N'�����㹻���Ĺ̶����壨ֱ��l���ϣ�����MN// l.��֪��K�����˶������˶�·����AB��BC��CD��DA��AC��BD������������˶�ʱ��Ϊx��M'N'�ij���Ϊy����y����x�ĺ���ͼ�������ͼ2��ʾ�����K���˶�·������Ϊ�� ��
A. A��B��C��D��A B. B��C��D��A��B
C. B��C��A��D��B D. D��A��B��C��D
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
С���������һ�����⣺��ͼ1������ABC�У���ACB=90�㣬BE��AC���ϵ����ߣ���D��BC���ϣ�CD��BD=1��2��AD��BE�ཻ�ڵ�P����![]() ��ֵ��
��ֵ��
С껷��֣�����A��AF��BC����BE���ӳ����ڵ�F��ͨ��������AEF�����������ͼ����ܹ�ʹ����õ��������ͼ2������ش���![]() ��ֵΪ����
��ֵΪ����
�ο�С�˼������ķ�����������⣺
��ͼ 3������ABC�У���ACB=90������D��BC���ӳ����ϣ�AD��AC���ϵ�����BE���ӳ��߽��ڵ�P��DC��BC��AC=1��2��3 ��
��1����![]() ��ֵ��
��ֵ��
��2����CD=2����BP=__________��
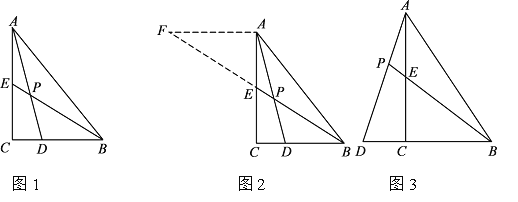
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABCD�ĶԽ���AC��BD���ڵ�O����֤��AB2+BC2+CD2+DA2=AC2+BD2.
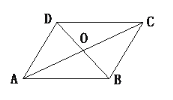
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ1��ƽ��ֱ������ϵxOy�У��ı���OABC�Ǿ��Σ���A��C������ֱ�Ϊ��6��0������0��2������D���߶�BC�ϵ�һ�����㣨��D���B��C���غϣ�������D��ֱ��y����![]() x��b������O��A��B�ڵ�E.
x��b������O��A��B�ڵ�E.
��1���ڵ�D�˶��Ĺ����У�����ODE�����ΪS����S��b�ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��2����ͼ2������E���߶�OA��ʱ������OABC����ֱ��DE�ԳƵ�ͼ��Ϊ����O��A��B��C�䣬C��B���ֱ�CB��OA�ڵ�D��M��O��A���ֱ�CB��OA�ڵ�N��E����֤���ı���DMEN�����Σ�
��3�����⣨2���е��ı���DMEN�У�ME�ij�Ϊ____________��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ijУ���꼶����������������Ӹ�У���꼶��ȡ50����������1�����������ԣ�������������������Ƶ���ֲ�ֱ��ͼ����֪ͼ�д����ҵ�һ���ڶ�������������С���Ƶ���ı�Ϊ1��3��4��2��

��1�������� �������� ������������ ��
��2�������С���Ƶ����Ƶ�ʣ�
��3��������ȡ��50�������У�1��������������100�����ϣ���100�Σ�������ռ����ȡ�����������İٷֱȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com