
【题目】阅读下面材料:
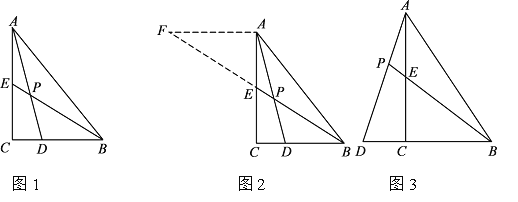
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.
的值.
小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:![]() 的值为 .
的值为 .
参考小昊思考问题的方法,解决问题:
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求![]() 的值;
的值;
(2)若CD=2,则BP=__________.
【答案】![]() 的值为
的值为![]() ;(1)
;(1)![]() ;(2) 6.
;(2) 6.
【解析】试题分析:易证△AEF≌△CEB,则有AF=BC.设CD=k,则DB=2k,AF=BC=3k,由AF∥BC可得△APF∽△DPB,然后根据相似三角形的性质就可求出![]() 的值;
的值;
解决问题:(1)过点A作AF∥DB,交BE的延长线于点F,设DC=k,由DC:BC=1:2得BC=2k,DB=DC+BC=3k.易证△AEF≌△CEB,则有EF=BE,AF=BC=2k.易证△AFP∽△DBP,然后根据相似三角形的性质就可求出![]() 的值;
的值;
(2)当CD=2时,可依次求出BC、AC、EC、EB、EF、BF的值,然后根据![]() 的值求出
的值求出![]() ,就可求出BP的值.
,就可求出BP的值.
试题解析:解:![]() 的值为
的值为![]() .
.
易证△AEF≌△CEB,则有AF=BC.
设CD=k,则DB=2k,AF=BC=3k,由AF∥BC可得△APF∽△DPB,即可得到![]() =
=![]() =
=![]() .故答案为:
.故答案为:![]() ;
;
解决问题:
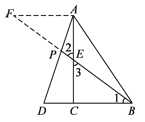
(1)过点A作AF∥DB,交BE的延长线于点F,如图,设DC=k,由DC:BC=1:2得BC=2k,DB=DC+BC=3k.∵E是AC中点,∴AE=CE.∵AF∥DB,∴∠F=∠1.
在△AEF和△CEB中,∵∠F=∠1,∠2=∠3,AE=CE,∴△AEF≌△CEB,∴EF=BE,AF=BC=2k.∵AF∥DB,∴△AFP∽△DBP,∴![]() =
=![]() ,∴
,∴![]() 的值为
的值为![]() ;
;
(2)当CD=2时,BC=4,AC=6,∴EC=![]() AC=3,EB=
AC=3,EB=![]() =5,∴EF=BE=5,BF=10.∵
=5,∴EF=BE=5,BF=10.∵![]() (已证),∴
(已证),∴![]() ,∴BP=
,∴BP=![]() BF=
BF=![]() ×10=6.
×10=6.
故答案为:6.


科目:初中数学 来源: 题型:
【题目】(1)解不等式2(4x-1)≥5x-8,并把它的解集在数轴上表示出来.
![]()
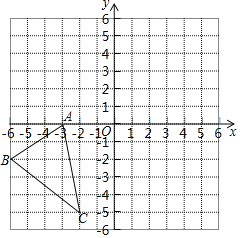
(2)如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别是A(-3,0),B(-6,-2)C(-2,-5).将△ABC向上平移3个单位长度,再向右平移5个单位长度,得到△A1B1C1.
①在平面直角坐标系xOy中画出△A1B1C1.
②求△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).
(1)求该反比例函数的表达式;
(2)求直线BC的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点D,E在AC的同侧,∠A=∠C=90°,BD⊥BE,AD=BC.
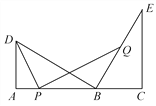
(1)求证:AC=AD+CE;
(2)若AD=3,AB=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q,当点P与A,B两点不重合时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级举行英语演讲比赛,准备用1200元钱(全部用完)购买A,B两种笔记本作为奖品,已知A,B两种每本分别为12元和20元,设购入A种x本,B种y本.
(1)求y关于x的函数表达式.
(2)若购进A种的数量不少于B种的数量.
①求至少购进A种多少本?
②根据①的购买,发现B种太多,在费用不变的情况下把一部分B种调换成另一种C,调换后C种的数量多于B种的数量,已知C种每本8元,则调换后C种至少有______本(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(甲)是四边形纸片 ABCD,其中∠B=130°,∠D=50°.若将其右下角向内折出△PCR,恰使CP∥AB,RC∥AD,如图(乙)所示,则∠C=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
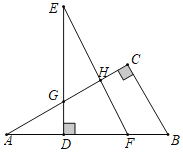
【题目】如图,在Rt△ABC中,∠C=90°,点D是AB边上一点,DE⊥AB,且DE=AC,DE与AC交于点G,过点E作FE∥BC交AB于点F,交AC于点H.
(1)求证:△ABC≌△EFD;
(2)若∠EFD=55°,求∠DGH的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,B、D、E、F是直线 l上四点,在直线 l的同侧作△ABE和△CDF,且 AB∥CD,∠A=40°.作BG⊥AE于 G,FH⊥CD于 H,BG与 FH交于 P点.
(1)如图 1,B、E、D、F从左至右顺次排列,∠ABD=90°,求∠GPH;
(2)如图 2,B、E、D、F从左至右顺次排列,△ABE与△CDF均为锐角三角形,求∠GPH;
(3)如图 3,F、B、E、D从左至右顺次排列,△ABE为锐角三角形,△CDF为钝角三角形,则∠GPH的度 数为多少?请画出图形并直接写出结果,不需证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于G,连接AG、HG.下列结论:①CE⊥DF;②AG=DG;③∠CHG=∠DAG;④2HG=AD.正确的有( )
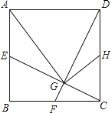
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com