
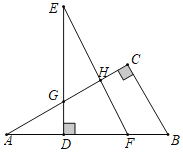
【题目】如图,在Rt△ABC中,∠C=90°,点D是AB边上一点,DE⊥AB,且DE=AC,DE与AC交于点G,过点E作FE∥BC交AB于点F,交AC于点H.
(1)求证:△ABC≌△EFD;
(2)若∠EFD=55°,求∠DGH的度数.
科目:初中数学 来源: 题型:
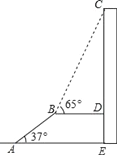
【题目】如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin65°≈
,sin65°≈![]() ,tan65°≈
,tan65°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ACB与∠CAB的平分线交于点P,PD⊥AB于点D,若△APC与△APD的周长差为![]() ,四边形BCPD的周长为12+
,四边形BCPD的周长为12+![]() ,则BC等于______.
,则BC等于______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
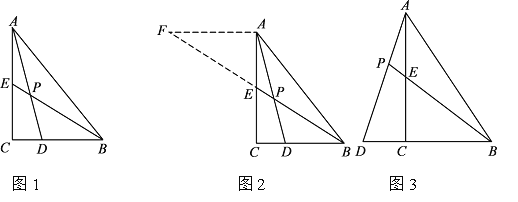
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.
的值.
小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:![]() 的值为 .
的值为 .
参考小昊思考问题的方法,解决问题:
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求![]() 的值;
的值;
(2)若CD=2,则BP=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
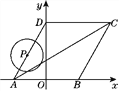
【题目】如图,菱形ABCD的顶点A,B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,∠BAD=60°,点A的坐标为(-2,0).
(1)求线段AD所在直线的表达式;
(2)动点P从点A出发,以每秒1个单位长度的速度,按照A→D→C→B→A的顺序在菱形的边上匀速运动一周,设运动时间为t秒.求t为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,平面直角坐标系xOy中,四边形OABC是矩形,点A,C的坐标分别为(6,0),(0,2).点D是线段BC上的一个动点(点D与点B,C不重合),过点D作直线y=-![]() x+b交折线O-A-B于点E.
x+b交折线O-A-B于点E.
(1)在点D运动的过程中,若△ODE的面积为S,求S与b的函数关系式,并写出自变量的取值范围;
(2)如图2,当点E在线段OA上时,矩形OABC关于直线DE对称的图形为矩形O′A′B′C′,C′B′分别交CB,OA于点D,M,O′A′分别交CB,OA于点N,E.求证:四边形DMEN是菱形;
(3)问题(2)中的四边形DMEN中,ME的长为____________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为1的正![]() 的顶点
的顶点![]() 在原点,点
在原点,点![]() 在
在![]() 轴负半轴上,正方形
轴负半轴上,正方形![]() 边长为2,点
边长为2,点![]() 在
在![]() 轴正半轴上,动点
轴正半轴上,动点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿着
出发,以每秒1个单位的速度沿着![]() 的边按逆时针方向运动,动点
的边按逆时针方向运动,动点![]() 从
从![]() 点出发,以每秒1个单位的速度沿着正方形
点出发,以每秒1个单位的速度沿着正方形![]() 的边也按逆时针方向运动,点
的边也按逆时针方向运动,点![]() 比点
比点![]() 迟1秒出发,则点
迟1秒出发,则点![]() 运动2016秒后,则
运动2016秒后,则![]() 的值是___________.
的值是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
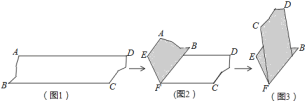
A.120°B.108°C.126°D.114°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com