
【题目】如图,B、D、E、F是直线 l上四点,在直线 l的同侧作△ABE和△CDF,且 AB∥CD,∠A=40°.作BG⊥AE于 G,FH⊥CD于 H,BG与 FH交于 P点.
(1)如图 1,B、E、D、F从左至右顺次排列,∠ABD=90°,求∠GPH;
(2)如图 2,B、E、D、F从左至右顺次排列,△ABE与△CDF均为锐角三角形,求∠GPH;
(3)如图 3,F、B、E、D从左至右顺次排列,△ABE为锐角三角形,△CDF为钝角三角形,则∠GPH的度 数为多少?请画出图形并直接写出结果,不需证明.

【答案】(1)40°;(2)140°;(3)40°.
【解析】
(1)由题意可根据直角三角形两锐角互余求出∠GPH=∠A=40°;
(2)延长CD与AE相交于点M,则PGMH为四边形,因为BG⊥AE于G,FH⊥CD于H,则∠PGE=∠PHD=90°,则∠P=360°-∠PGE°-∠PHD-∠M=360°-180°-∠M,又知AB∥CD,所以∠M=∠A=40°,则可以求得∠P的度数;
(3)根据题意可以作图,延长AB与FH相交于点M,因为AB∥CD,所以∠CHF=∠BMP=90°,则根据三角形内角和定理可得∠GPH=∠A=40°.
(1)∵BG⊥AE,
∴∠BGE=90°
∴∠GBE+∠GEB=90°
∵FH⊥CD, AB∥CD,
∴AB⊥BE,
∴∠ABE=90°
∴∠A+∠AEB=90°,
∴∠GPH=∠GBE=∠A=40°;
(2)如图所示:

∵AB∥CD,
∴∠M=∠A=40°.
延长CD与AE相交于点M.
则在四边形PGMH中∠P=360°-180°-∠M=360°-∠A-180°=140°;
(3)∠GPH=40°,图如下边所示:
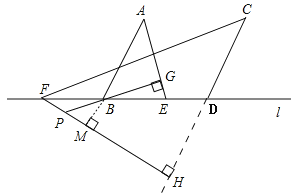
延长AB与FH相交于点M,
因为AB∥CD,
所以∠CHF=∠BMP=90°,
∵PG⊥AE,
∴∠BAG+∠ABG=90°,∠PBM+∠BPM=90°,
∵∠ABG=∠PBM,
∴∠BPM=∠A,
即∠GPH=∠A=40°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
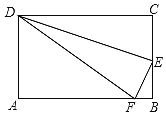
【题目】如图所示,沿DE折叠长方形ABCD的一边,使点C落在AB边上的点F处,若AD=8,且△AFD的面积为60,则△DEC的面积为( )
A. ![]()
B. ![]()
C. 18
D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
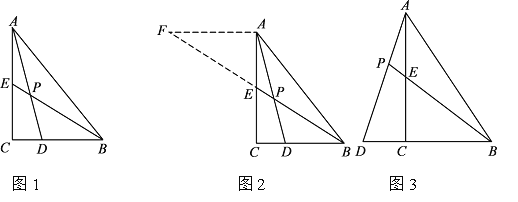
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.
的值.
小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:![]() 的值为 .
的值为 .
参考小昊思考问题的方法,解决问题:
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求![]() 的值;
的值;
(2)若CD=2,则BP=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
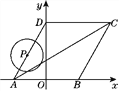
【题目】如图,菱形ABCD的顶点A,B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,∠BAD=60°,点A的坐标为(-2,0).
(1)求线段AD所在直线的表达式;
(2)动点P从点A出发,以每秒1个单位长度的速度,按照A→D→C→B→A的顺序在菱形的边上匀速运动一周,设运动时间为t秒.求t为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,平面直角坐标系xOy中,四边形OABC是矩形,点A,C的坐标分别为(6,0),(0,2).点D是线段BC上的一个动点(点D与点B,C不重合),过点D作直线y=-![]() x+b交折线O-A-B于点E.
x+b交折线O-A-B于点E.
(1)在点D运动的过程中,若△ODE的面积为S,求S与b的函数关系式,并写出自变量的取值范围;
(2)如图2,当点E在线段OA上时,矩形OABC关于直线DE对称的图形为矩形O′A′B′C′,C′B′分别交CB,OA于点D,M,O′A′分别交CB,OA于点N,E.求证:四边形DMEN是菱形;
(3)问题(2)中的四边形DMEN中,ME的长为____________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年“519(我要走)全国徒步日(江夏站)”暨第六届“环江夏”徒步大会5月19日在美丽的花山脚下降重举行.组委会(活动主办方)为了奖励活动中取得了好成绩的参赛选手,计划购买共100件的甲、乙两种纪念品发放.其中甲种纪念品每件售价120元,乙种纪念品每件售价80元.
(1)如果购买甲、乙两种纪念品一共花费了9600元,求购买甲、乙两种纪念品各是多少件?
(2)设购买甲种纪念品![]() 件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为1的正![]() 的顶点
的顶点![]() 在原点,点
在原点,点![]() 在
在![]() 轴负半轴上,正方形
轴负半轴上,正方形![]() 边长为2,点
边长为2,点![]() 在
在![]() 轴正半轴上,动点
轴正半轴上,动点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿着
出发,以每秒1个单位的速度沿着![]() 的边按逆时针方向运动,动点
的边按逆时针方向运动,动点![]() 从
从![]() 点出发,以每秒1个单位的速度沿着正方形
点出发,以每秒1个单位的速度沿着正方形![]() 的边也按逆时针方向运动,点
的边也按逆时针方向运动,点![]() 比点
比点![]() 迟1秒出发,则点
迟1秒出发,则点![]() 运动2016秒后,则
运动2016秒后,则![]() 的值是___________.
的值是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(3,4),点B为直线x=1上的动点,设B(-1,y).

(1)如图①,若△ABO是等腰三角形且AO=AB时,求点B的坐标;
(2)如图②,若点C(x,0)且-1<x<3,BC⊥AC垂足为点C;
①当x=0时,求tan∠BAC的值;
②若AB与y轴正半轴的所夹锐角为α,当点C在什么位置时tanα的值最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=8,BC=12,点D从B出发以每秒2个单位的速度在线段BC上从过点B向点C运动,点E同时从点C出发,以每秒2个单位的速度在线段AC上从点A运动,连接AD、DE,设D、E两点运动时间为![]() 秒.
秒.
(1)运动_____秒时,CD=3AE.
(2)运动多少秒时,△ABD≌△DCE能成立,并说明理由;
(3)若△ABD≌△DCE,∠BAC=![]() 则∠ADE=_______(用含
则∠ADE=_______(用含![]() 的式子表示)。
的式子表示)。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com