
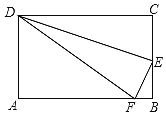
【题目】如图所示,沿DE折叠长方形ABCD的一边,使点C落在AB边上的点F处,若AD=8,且△AFD的面积为60,则△DEC的面积为( )
A. ![]()
B. ![]()
C. 18
D. 20
【答案】A
【解析】
由矩形的性质得出∠A=∠B=90°,BC=AD=8,CD=AB,结合△AFD的面积为60,即可求得AF与DF的长,由折叠的性质,可得CD=DF,然后在Rt△BEF中,利用勾股定理即可求得CE的长,继而求得△DEC的面积.
∵四边形ABCD是矩形,
∴∠A=∠B=90°,BC=AD=8,CD=AB,
∵△AFD的面积为60,
即![]() ADAF=60,
ADAF=60,
解得:AF=15,
∴DF=![]() =
=![]() =17,
=17,
由折叠的性质,得:CD=DF=17,
∴AB=17,
∴BF=AB-AF=17-15=2,
设CE=x,则EF=CE=x,BE=BC-CE=8-x,
在Rt△BEF中,EF2=BF2+BE2,
即x2=22+(8-x)2,
解得:x=![]() ,
,
即CE=![]() ,
,
∴△DEC的面积=![]() CDCE=
CDCE=![]() ×17×
×17×![]() =
=![]() ;
;
故选A.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】随着越来越多年轻家长对低幼阶段孩子英语口语的重视,某APP顺势推出了“北美外教在线授课”系列课程,提供“A课程”、“B课程”两种不同课程供家长选择.已知购买“A课程”3课时与“B课程”5课时共需付款410元,购买“A课程”5课时与“B课程”3课时共需付款470元.
(1)请问购买“A课程”1课时多少元?购买“B课程”1课时多少元?
(2)根据市场调研,APP销售“A课程”1课时获利25元,销售“B课程”1课时获利20元,临近春节,小融计划用不低于3000元且不超过3600元的压岁钱购买两种课程共60课时,请问购买“A课程”多少课时才使得APP的获利最高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解不等式2(4x-1)≥5x-8,并把它的解集在数轴上表示出来.
![]()
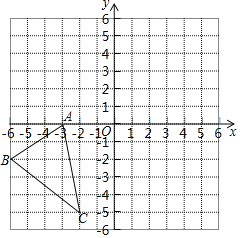
(2)如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别是A(-3,0),B(-6,-2)C(-2,-5).将△ABC向上平移3个单位长度,再向右平移5个单位长度,得到△A1B1C1.
①在平面直角坐标系xOy中画出△A1B1C1.
②求△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开设武术、舞蹈、剪纸等三项活动课程以提升学生的体艺素养,随机抽取了部分学生对这三项活动的兴趣情况进行了调查(每人从中只能选一项),并将调查结果绘制成如图两幅统计图,请你结合图中信息解答问题.
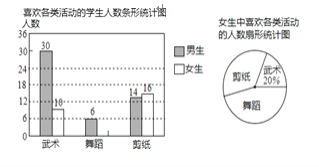
(1)将条形统计图补充完整;
(2)本次抽样调查的样本容量是 ;
(3)已知该校有1200名学生,请你根据样本估计全校学生中喜欢剪纸的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车在行驶的过程中速度往往是变化的,如图表示一辆汽车的速度随时间变化而变化的情况.
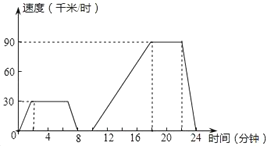
(1)汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?
(2)汽车在哪些时间段保持匀速行驶?时速分别是多少?
(3)汽车出发8min到10min之间可能发生了什么情况?
(4)求汽车从出发后第18分钟到第22分钟行驶的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
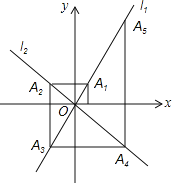
【题目】如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过A1点作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2019的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).
(1)求该反比例函数的表达式;
(2)求直线BC的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点D,E在AC的同侧,∠A=∠C=90°,BD⊥BE,AD=BC.
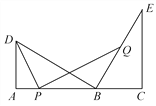
(1)求证:AC=AD+CE;
(2)若AD=3,AB=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q,当点P与A,B两点不重合时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,B、D、E、F是直线 l上四点,在直线 l的同侧作△ABE和△CDF,且 AB∥CD,∠A=40°.作BG⊥AE于 G,FH⊥CD于 H,BG与 FH交于 P点.
(1)如图 1,B、E、D、F从左至右顺次排列,∠ABD=90°,求∠GPH;
(2)如图 2,B、E、D、F从左至右顺次排列,△ABE与△CDF均为锐角三角形,求∠GPH;
(3)如图 3,F、B、E、D从左至右顺次排列,△ABE为锐角三角形,△CDF为钝角三角形,则∠GPH的度 数为多少?请画出图形并直接写出结果,不需证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com