
【题目】随着越来越多年轻家长对低幼阶段孩子英语口语的重视,某APP顺势推出了“北美外教在线授课”系列课程,提供“A课程”、“B课程”两种不同课程供家长选择.已知购买“A课程”3课时与“B课程”5课时共需付款410元,购买“A课程”5课时与“B课程”3课时共需付款470元.
(1)请问购买“A课程”1课时多少元?购买“B课程”1课时多少元?
(2)根据市场调研,APP销售“A课程”1课时获利25元,销售“B课程”1课时获利20元,临近春节,小融计划用不低于3000元且不超过3600元的压岁钱购买两种课程共60课时,请问购买“A课程”多少课时才使得APP的获利最高?
【答案】(1)购买“A课程”1课时70元,购买“B课程”1课时40元;(2)购买“A课程”40课时.
【解析】
(1)根据题意,购买“A课程”3课时与“B课程”5课时共需付款410元,购买“A课程”5课时与“B课程”3课时共需付款470元,列出二元一次方程组求解即可;
(2)根据题意,小融计划用不低于3000元且不超过3600元的压岁钱购买两种课程共60课时,可列出一元一次不等式组求解.
解:(1)设购买“A课程”1课时x元,购买“B课程”1课时y元.
依题意,得:![]() ,
,
解得:![]() ,
,
答:购买“A课程”1课时70元,购买“B课程”1课时40元.
(2)设购买“A课程”a 课时,则购买“B课程”60﹣a 课时.
依题意,得:![]() ,
,
解得:20≤a≤40,
设利润为w,
w=25a+20(60﹣a)=5a+1200,
∵5>0,∴w随着a的增大而增大,
故当a=40时,w最大.
答:购买“A课程”40课时才使得APP的获利最高.
故答案为:(1)购买“A课程”1课时70元,购买“B课程”1课时40元;(2)购买“A课程”40课时.


科目:初中数学 来源: 题型:
【题目】三角形角平分线交点或三角形内切圆的圆心都称为三角形的内心.按此说法,四边形的四个角平分线交于一点,我们也称为“四边形的内心”.
(1)试举出一个有内心的四边形.
(2)探究:对于任意四边形ABCD,如果有内心,则四边形的边长具备何种条件?为什么?
(3)探究:腰长为![]() 的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?
的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?
(4)问题(3)中,O是四边形ABDE内心,且四边形ABDE是等腰梯形,求DE的长?
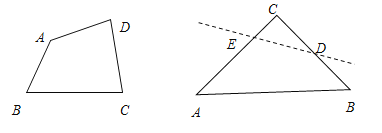
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形。若![]() ,AB=2,则图中阴影部分的面积为( )
,AB=2,则图中阴影部分的面积为( )

A. 12-4![]() B. 5 C. 12-4
B. 5 C. 12-4![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题.
如图,![]() 、
、![]() 分别为数轴上的两点,
分别为数轴上的两点,![]() 点对应的数为
点对应的数为![]() ,
,![]() 点对应的数为
点对应的数为![]() .
.

(![]() )请写出与
)请写出与![]() 、
、![]() 两点距离相等的点
两点距离相等的点![]() 所对应的数.
所对应的数.
(![]() )现有一只电子蚂蚁
)现有一只电子蚂蚁![]() 从
从![]() 点出发,以
点出发,以![]() 单位/秒的速度向左运动,同时另一只电子蚂蚁
单位/秒的速度向左运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以
点出发,以![]() 单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的
单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的![]() 点相遇,你知道
点相遇,你知道![]() 点对应的数是多少吗?
点对应的数是多少吗?
(![]() )若当电子蚂蚁
)若当电子蚂蚁![]() 从
从![]() 点出发时,以
点出发时,以![]() 单位/秒的速度向左运动,同时另一只电子蚂蚁
单位/秒的速度向左运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以
点出发,以![]() 单位/秒的速度也向左运动,设两只电子蚂蚁在数轴上的
单位/秒的速度也向左运动,设两只电子蚂蚁在数轴上的![]() 点相遇,你知道
点相遇,你知道![]() 点对应的数是多少吗?
点对应的数是多少吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
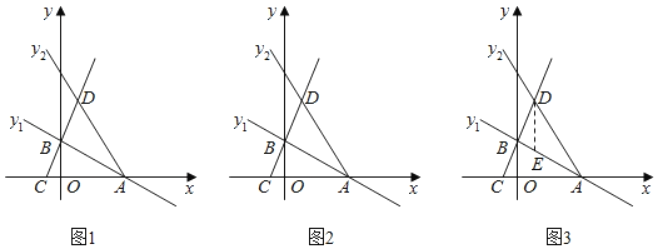
【题目】如图1,平面直角坐标系中,直线y1=﹣![]() x+3与x轴、y轴分别交于A、B两点,直线y2=﹣2x+b经过点A,已知点C(﹣1,0),直线BC与直线y2相交于点D.
x+3与x轴、y轴分别交于A、B两点,直线y2=﹣2x+b经过点A,已知点C(﹣1,0),直线BC与直线y2相交于点D.
(1)请直接写出:A点坐标为 ,直线BC解析式为 ,D点坐标为 ;
(2)若线段OA在x轴上移动,且点O,A移动后的对应点为O1、A1,首尾顺次连接点O1、A1、D、B构成四边形O1A1DB,当四边形O1A1DB的周长最小时,y轴上是否存在点M,使|A1M﹣DM|有最大值,若存在,请求出此时M的坐标;若不存在请说明理由.
(3)如图3,过点D作DE∥y轴,与直线AB交于点E,若Q为线段AD上一动点,将△DEQ沿边EQ翻折得到直线AB上方的△D′EQ,是否存在点Q使得△D′EQ与△AEQ的重叠部分图形为直角三角形,若存在,请求出DQ的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,D、F分别为BC、AB边上的点,AF=BD,以AD为边作等边ΔADE.
(1)求证:AE=CF;
(2)求∠BEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
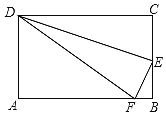
【题目】如图所示,沿DE折叠长方形ABCD的一边,使点C落在AB边上的点F处,若AD=8,且△AFD的面积为60,则△DEC的面积为( )
A. ![]()
B. ![]()
C. 18
D. 20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com