【题目】探究题．
如图，
、
分别为数轴上的两点，点对应的数为
，点对应的数为
．
（
）请写出与、两点距离相等的点
所对应的数．
（
）现有一只电子蚂蚁
从点出发，以
单位/秒的速度向左运动，同时另一只电子蚂蚁
恰好从点出发，以
单位/秒的速度向右运动，设两只电子蚂蚁在数轴上的
点相遇，你知道点对应的数是多少吗？
（
）若当电子蚂蚁从点出发时，以单位/秒的速度向左运动，同时另一只电子蚂蚁恰好从点出发，以单位/秒的速度也向左运动，设两只电子蚂蚁在数轴上的
点相遇，你知道点对应的数是多少吗？
【答案】（1）40；（2）28；（3）-260
【解析】
(1)求-20与100和的一半即是M；
(2)此题是相遇问题,先求出相遇所需的时间,再求出点Q走的路程，根据“左减右加”的原则，可求出-20向右运动到相遇地点所对应的数；
(3)此题是追及问题,可先求出P追上Q所需的时间，然后可求出Q所走的路程，根据“左减右加”的原则，可求出点D所对应的数。
因为A、B分别是数轴上的两点，
点对应的数为
，
点对应的数为
则AB中点M对应的数是100-60=40
即M点对应的数是40；
(2)由题意知P与Q的相遇时间是
所以相同时间Q点运动的路程为
即从数-20向右运动48个单位到数28；
(3) P点追到Q点的时间为
所以此时Q点起过路程为
即从数-20向左运动240个单位到数-260.
科目：初中数学 来源： 题型：
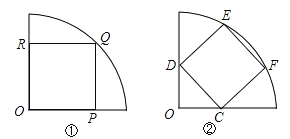
【题目】有一批圆心角为90o，半径为3的扇形下脚料，现利用这批材料截取尽可能大的正方形材料，如图有两种截取方法：
方法一：如图1所示，正方形OPQR的顶点P、Q、R均在扇形的边界上；
方法二：如图2所示，正方形顶点C、D、E、F均在扇形边界上．
试分别求这两种截取方法得到的正方形面积，并说明哪种截取方法得到的正方形面积更大．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点
，
之间有一条曲线和一条线段，
在线段
上，己知
，
，
是线段
上一动点，过点作
交曲线于点
，连接
，过点作
于点
．设，两点间的距离为
，，两点间的距离为
．（当点与点重合时，
的值为
）小思根据学习函数的经验，对函数随自变量
的变化而变化的规律进行了探究．
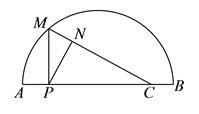
下面是小思的探究过程，请补充完整：
（
）通过取点，画图，测量，得到了与的几组值，补全下表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（说明：补全表格时相关数值保留一位小数）
（
）在下列平面直角坐标系中描出以补全后的表中各对对应值为坐标的点，画出该函数的图象．
（
）结合画出的函数图象，解决问题：当
时，
的长度约为__________
（结果保留一位小数）．
查看答案和解析>>
科目：初中数学 来源： 题型：
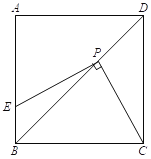
【题目】如图，正方形ABCD的边长为6，点E是边AB上一点，点P是对角线BD上一点，且PE⊥PC．
⑴ 求证：PC＝PE；
⑵ 若BE＝2，求PB的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
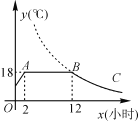
【题目】我市某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种．如图是某天恒温系统从开启到关闭及关闭后，大棚内温度y(℃)随时间x(小时)变化的函数图象，其中BC段是双曲线y=
的一部分．请根据图中信息解答下列问题：
(1)恒温系统在这天保持大棚内温度18 ℃的时间有多少小时？
(2)求k的值；
(3)当x＝16时，大棚内的温度约为多少度？
查看答案和解析>>
科目：初中数学 来源： 题型：
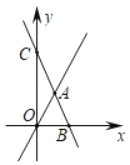
【题目】已知直线l1：y＝kx过点（1，2），与直线l2：y＝﹣3x+b相交于点A，若l2与x轴交于点B（2，0），与y轴交于点C．
（1）分别求出直线11，l2的解析式；
（2）求△OAC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】随着越来越多年轻家长对低幼阶段孩子英语口语的重视，某APP顺势推出了“北美外教在线授课”系列课程，提供“A课程”、“B课程”两种不同课程供家长选择．已知购买“A课程”3课时与“B课程”5课时共需付款410元，购买“A课程”5课时与“B课程”3课时共需付款470元．
（1）请问购买“A课程”1课时多少元？购买“B课程”1课时多少元？
（2）根据市场调研，APP销售“A课程”1课时获利25元，销售“B课程”1课时获利20元，临近春节，小融计划用不低于3000元且不超过3600元的压岁钱购买两种课程共60课时，请问购买“A课程”多少课时才使得APP的获利最高？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD平分∠BAC,按如下步骤作图：第一步，分别以点A、D为圆心，以大于
的长为半径在AD的两侧作弧，交于两点M、N;第二步，连结MN，分别交AB、AC于点E、F；第三步，连结DE、DF．．若BD=6，AF=4，CD=3，则BE的长是（ ）
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了开设武术、舞蹈、剪纸等三项活动课程以提升学生的体艺素养，随机抽取了部分学生对这三项活动的兴趣情况进行了调查（每人从中只能选一项），并将调查结果绘制成如图两幅统计图，请你结合图中信息解答问题．
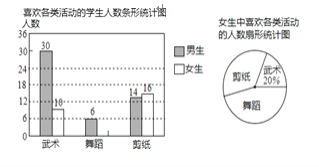
（1）将条形统计图补充完整；
（2）本次抽样调查的样本容量是 ；
（3）已知该校有1200名学生，请你根据样本估计全校学生中喜欢剪纸的人数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
