
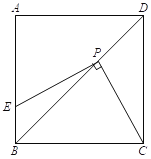
【题目】如图,正方形ABCD的边长为6,点E是边AB上一点,点P是对角线BD上一点,且PE⊥PC.
⑴ 求证:PC=PE;
⑵ 若BE=2,求PB的长.
【答案】(1)证明见解析;(2)![]()
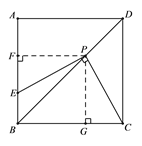
【解析】分析: ![]() 过点P作PF⊥AB,PG⊥BC,垂足分别为点F、G.证明△PFE≌△PGC即可.
过点P作PF⊥AB,PG⊥BC,垂足分别为点F、G.证明△PFE≌△PGC即可.
![]() 设EF=x.根据 △PFE≌△PGC .得到GC=EF=x. 由BE=2得:BF=x+2.
设EF=x.根据 △PFE≌△PGC .得到GC=EF=x. 由BE=2得:BF=x+2.
由正方形FBGP得:BG=x+2. BG+GC=6.列出方程,求出![]() ,在△PFB中,用勾股定理即可求出PB的长.
,在△PFB中,用勾股定理即可求出PB的长.
详解:⑴ 过点P作PF⊥AB,PG⊥BC,垂足分别为点F、G.
∴ ∠PFB=∠PGB=∠PGC=90°,
∵ 四边形ABCD是正方形,
∴ ∠A=∠ABC=90°,AB=AD=BC,
∴ ∠ABD=∠ADB=45°,四边形FBGP是矩形,
∴ ∠FPB=90°-∠ABD=90°-45°=45°,
∴ ∠ABD=∠FPB,
∴ FP=FB,
∴ 矩形FBGP是正方形,
∴ PF=PG,∠FPG=90°,
∴ ∠FPG+∠EPG=90°,
∵ EP⊥PC,
∴ ∠EPC=90°,
∴ ∠GPC+∠EPG=90°,
∴ ∠FPG=∠GPC ,
∵ ∠FPG=∠GPC ,PF=PG,∠PFE=∠PGC,
∴△PFE≌△PGC(ASA)
∴ PE=PC.
 (方法不唯一,酌情给分)
(方法不唯一,酌情给分)
⑵ 设EF=x.
∵ △PFE≌△PGC .
∴ GC=EF=x.
由BE=2得:BF=x+2.
由正方形FBGP得:BG=x+2.
∵ BC=6,
∴ BG+GC=6.
∴ (x+2)+x=6,
解得:x=2.
∴ PF=BF=2+2=4 ,
△PFB中,∠PFB=90°,由勾股定理得: ![]() ,
,
∵ PB>0
∴![]()
答:PB的长为![]()


科目:初中数学 来源: 题型:
【题目】将下列各数填入相应的括号里:
![]() ,5,
,5,![]() ,
,![]() ,0,8,-2,-0.7
,0,8,-2,-0.7![]() ……
……
正数集合{________________________________________…};
负数集合{________________________________________…};
有理数集合{________________________________________…};
无理数集合{________________________________________…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( ) 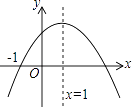
A.a>0
B.3是方程ax2+bx+c=0的一个根
C.a+b+c=0
D.当x<1时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,并且AF=CE.
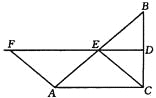
(1)求证:四边形ACEF是平行四边形;
(2)当∠B的大小满足什么条件时,四边形ACEF是菱形?请回答并证明你的结论;
(3)四边形ACEF有可能是正方形吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC放置在第一象限内,顶点A在x轴上,若顶点B的坐标是(4,3),(1)请求出菱形边长OA的长度.
(2)反比例函数![]() 经过点C,请求出
经过点C,请求出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值,
(1)2x2y﹣[3xy2+2(xy2+2x2y)],其中x=![]() ,y=﹣2.
,y=﹣2.
(2)已知a+b=4,ab=﹣2,求代数式(4a﹣3b﹣2ab)﹣(a﹣6b﹣ab)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列给出四个命题:
①直角三角形的两边是方程y2-7y+12=0的两根,则它的第三边是5;
②若一元二次方程ax2+bx+c=0(a≠0)的系数a,c异号,则该方程有两个不相等的实数根;
③若一元二次方程(m-2)x2+x+m2-4=0有一个根为0,那么m=±2;
④已知一元二次方程ax2+bx+c=0(a≠0)中a,b,c满足a-b+c=0,4a+2b+c=0则方程的两根为x1=-1,x2=2;其中真命题的是__________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的顶点坐标为A(﹣2,3)、B(﹣3,1)、C(﹣1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C′,点B′、C′分别是点B、C的对应点. 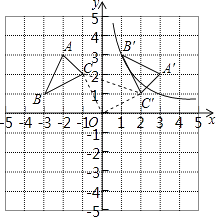
(1)求过点B′的反比例函数解析式;
(2)求线段CC′的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com