
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,并且AF=CE.
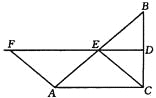
(1)求证:四边形ACEF是平行四边形;
(2)当∠B的大小满足什么条件时,四边形ACEF是菱形?请回答并证明你的结论;
(3)四边形ACEF有可能是正方形吗?为什么?
【答案】(1)、证明过程见解析;(2)、∠B=30°,证明过程见解析;(3)、不可能,理由见解析.
【解析】试题分析:(1)、根据DF为垂直平分线得出BD=CD,DF⊥BC,根据∠ACB=∠BDF=90°得出DF∥AC,则BE=AE,则AE=CE,∴∠1=∠2,得到△ACE≌△EFA,即AC=EF,从而得到平行四边形;(2)、当∠B=30°时,AC=![]() AB,CE=
AB,CE=![]() AB,从而得到AC=CE,得到菱形;(3)、根据CE在△ABC内部,∠ACE<∠ACB=90°,则不可能为正方形.
AB,从而得到AC=CE,得到菱形;(3)、根据CE在△ABC内部,∠ACE<∠ACB=90°,则不可能为正方形.
试题解析:(1)、∵DF是BC的垂直平分线 ∴DF⊥BC,DB=DC
∴∠ACB=∠BDF=90° ∴DF∥AC ∴BE="AE"
∴AE=CE=![]() AB
AB
∴∠1=∠2
∵EF∥BC,AF=CE=AE
∴∠1=∠2=∠3=∠F
∴△ACE≌△EFA ∴AC=EF
∴四边形ACEF是平行四边形;
(2)、当∠B=30°时,四边形ACEF是菱形.证明如下:
在△ABC中,∠ACB=90°,∠B=30°
∴AC=![]() AB ∵CE=
AB ∵CE=![]() AB ∴AC=CE
AB ∴AC=CE
∴四边形ACEF是菱形
(3)、四边形ACEF不可能是正方形,理由如下:由(1)知E是AB的中点
∴CE在△ABC内部,∴∠ACE<∠ACB=90° ∴四边形ACEF不可能是正方形


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】已知y是关于x的一次函数,且当x=1时,y=﹣4;当x=2时,y=﹣6.
(1)求y关于x的函数表达式;
(2)若﹣2<x<4,求y的取值范围;
(3)试判断点P(a,﹣2a+3)是否在函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在数轴上标出数﹣4.5,﹣2,1,3.5所对应的点A,B,C,D;
(2)C,D两点间距离=_____;B,C两点间距离=_____;
(3)数轴上有两点M,N,点M对应的数为a,点N对应的数为b,那么M,N两点之间的距离=_____;
(4)若动点P,Q分别从点B,C同时出发,沿数轴负方向运动;已知点P的速度是每秒1个单位长度,点Q的速度是每秒2个单位长度,问①t为何值时P,Q两点重合?②t为何值时P,Q两点之间的距离为1?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣37)﹣(﹣47) (2)10﹣(﹣5)+(﹣9)+6.
(3))-7+13-6+20 (4)0.125+3![]() -(+3
-(+3![]() )+(﹣0.25)
)+(﹣0.25)
(5)﹣|﹣1|+|![]() ﹣
﹣![]() |+(﹣2).
|+(﹣2).
(6)1+(﹣2)+3+(﹣4)+…+2017+(﹣2018)+2019+(﹣2020)
(7)(﹣5![]() )+(﹣9
)+(﹣9![]() )+17
)+17![]() +(﹣3
+(﹣3![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴子A、B两点,与反比例函数y![]() 的图象交于C、D两点,DE⊥x轴于点E,已知点C的坐标是(6,-1),DE=3.
的图象交于C、D两点,DE⊥x轴于点E,已知点C的坐标是(6,-1),DE=3.
(1)求反比例函数与一次函数的关系式;
(2)根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值?

查看答案和解析>>
科目:初中数学 来源: 题型:
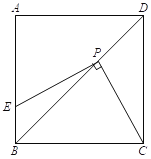
【题目】如图,正方形ABCD的边长为6,点E是边AB上一点,点P是对角线BD上一点,且PE⊥PC.
⑴ 求证:PC=PE;
⑵ 若BE=2,求PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了美化校园环境,在一块长40米,宽20米的长方形空地上计划新建一块长9米,宽7米的长方形花圃.
(1)若请你在这块空地上设计一个长方形花圃,使它的面积比学校计划新建的长方形花圃的面积多1平方米,请你给出你认为合适的三种不同的方案;
(2)在学校计划新建的长方形花圃周长不变的情况下,长方形花圃的面积能否增加2平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为﹣5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为![]() BC的点N,则该数轴的原点为( )
BC的点N,则该数轴的原点为( )
![]()
A. 点E B. 点F C. 点M D. 点N
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com