
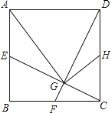
【题目】如图,正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于G,连接AG、HG.下列结论:①CE⊥DF;②AG=DG;③∠CHG=∠DAG;④2HG=AD.正确的有( )
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
连接AH,由四边形ABCD是正方形与点E、F、H分别是AB、BC、CD的中点,易证得△BCE≌△CDF与△ADH≌△DCF,根据全等三角形的性质,易证得CE⊥DF与AH⊥DF,根据垂直平分线的性质,即可证得AG=AD,由直角三角形斜边上的中线等于斜边的一半,即可证得2HG=AD,根据等腰三角形的性质,即可得∠CHG=∠DAG.则问题得解.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=90°,
∵点E、F、H分别是AB、BC、CD的中点,
∴BE=CF,
在△BCE与△CDF中
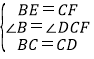 ,
,
∴△BCE≌△CDF,(SAS),
∴∠ECB=∠CDF,
∵∠BCE+∠ECD=90°,
∴∠ECD+∠CDF=90°,
∴∠CGD=90°,
∴CE⊥DF,故①正确;
在Rt△CGD中,H是CD边的中点,
∴HG=![]() CD=
CD=![]() AD,故④正确;
AD,故④正确;
连接AH,
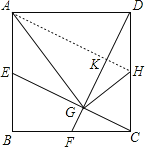
同理可得:AH⊥DF,
∵HG=HD=![]() CD,
CD,
∴DK=GK,
∴AH垂直平分DG,
∴AG=AD,故②错误;
∴∠DAG=2∠DAH,
同理:△ADH≌△DCF,
∴∠DAH=∠CDF,
∵GH=DH,
∴∠HDG=∠HGD,
∴∠GHC=∠HDG+∠HGD=2∠CDF,
∴∠CHG=∠DAG.故③正确.
故选C.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
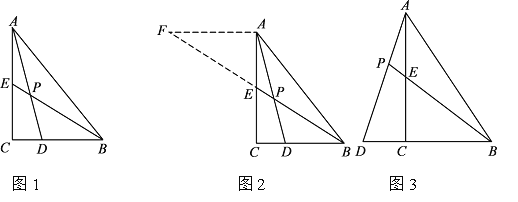
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.
的值.
小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:![]() 的值为 .
的值为 .
参考小昊思考问题的方法,解决问题:
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求![]() 的值;
的值;
(2)若CD=2,则BP=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为1的正![]() 的顶点
的顶点![]() 在原点,点
在原点,点![]() 在
在![]() 轴负半轴上,正方形
轴负半轴上,正方形![]() 边长为2,点
边长为2,点![]() 在
在![]() 轴正半轴上,动点
轴正半轴上,动点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿着
出发,以每秒1个单位的速度沿着![]() 的边按逆时针方向运动,动点
的边按逆时针方向运动,动点![]() 从
从![]() 点出发,以每秒1个单位的速度沿着正方形
点出发,以每秒1个单位的速度沿着正方形![]() 的边也按逆时针方向运动,点
的边也按逆时针方向运动,点![]() 比点
比点![]() 迟1秒出发,则点
迟1秒出发,则点![]() 运动2016秒后,则
运动2016秒后,则![]() 的值是___________.
的值是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(3,4),点B为直线x=1上的动点,设B(-1,y).

(1)如图①,若△ABO是等腰三角形且AO=AB时,求点B的坐标;
(2)如图②,若点C(x,0)且-1<x<3,BC⊥AC垂足为点C;
①当x=0时,求tan∠BAC的值;
②若AB与y轴正半轴的所夹锐角为α,当点C在什么位置时tanα的值最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校七年级男生的体能情况,从该校七年级抽取50名男生进行1分钟跳绳测试,把所得数据整理后,画出频数分布直方图.已知图中从左到右第一、第二、第三、第四小组的频数的比为1:3:4:2.

(1)总体是 ,个体是 ,样本容量是 ;
(2)求第四小组的频数和频率;
(3)求所抽取的50名男生中,1分钟跳绳次数在100次以上(含100次)的人数占所抽取的男生人数的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校七年级学生的数学作业完成情况,将完成情况分为四个等级:
随机对该年级若干名学生进行了调查,然后把调查结果绘制成两幅不完整的统计图.请根据图中的信息解答下列问题:
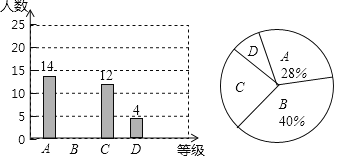
(1)共调查了多少名同学?补全条形统计图;
(2)完成等级为C等的对应扇形的圆心角的度数是 ;
(3)该年级共有700人,估计该年级数学作业完成等级为D等的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
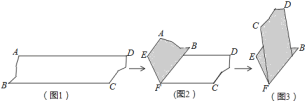
A.120°B.108°C.126°D.114°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=8,BC=12,点D从B出发以每秒2个单位的速度在线段BC上从过点B向点C运动,点E同时从点C出发,以每秒2个单位的速度在线段AC上从点A运动,连接AD、DE,设D、E两点运动时间为![]() 秒.
秒.
(1)运动_____秒时,CD=3AE.
(2)运动多少秒时,△ABD≌△DCE能成立,并说明理由;
(3)若△ABD≌△DCE,∠BAC=![]() 则∠ADE=_______(用含
则∠ADE=_______(用含![]() 的式子表示)。
的式子表示)。

查看答案和解析>>
科目:初中数学 来源: 题型:
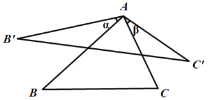
【题目】如图,将△ABC的边AB绕着点A顺时针旋转![]() (
(![]() )得到AB′,边AC绕着点A逆时针旋转
)得到AB′,边AC绕着点A逆时针旋转![]() (
(![]() )得到AC′,联结B′C′,当
)得到AC′,联结B′C′,当![]() +
+![]() =60°时,我们称
=60°时,我们称![]() AB′C′是
AB′C′是![]() ABC的“双旋三角形”,如果等边
ABC的“双旋三角形”,如果等边![]() ABC的边长为a, 那么它所得的“双旋三角形”中B′C′=___________(用含a的代数式表示).
ABC的边长为a, 那么它所得的“双旋三角形”中B′C′=___________(用含a的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com