
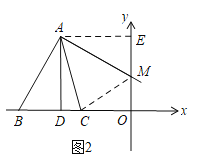
【题目】在平面直角坐标系中,点A的坐标为(-3,3),以A为顶点的∠BAC的两边始终与x轴交于B、C两点(B在C左面),且∠BAC=45°.过点A作AD⊥x轴,垂足为D,当DC=1时,将∠BAC沿AC所在直线翻折,翻折后边AB交y轴于点M,则点M的坐标是_____.
【答案】(0,1.5)或(0,-3)
【解析】
当点C在点D右侧时,连接CM,过点A作AE⊥y轴于点E,证明△BAD≌△MAE,在Rt△COM中,由勾股定理即可求得M的坐标;当点C在点D左侧时,连接CM,过点A作AF⊥y轴于点F,证明△BAD≌△MAF,同理,在Rt△COM中,由勾股定理即可求得M的坐标.
解:设OM=x,
当点C在点D右侧时,如图2,连接CM,过点A作AE⊥y轴于点E,
由∠BAM=∠DAE=90°,
可知:∠BAD=∠MAE;
∴在△BAD和△MAE中,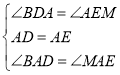 ,
,
∴△BAD≌△MAE.
∴BD=EM=3-x.
又∵AC=AC,∠BAC=∠MAC,
∴△BAC≌△MAC.
∴BC=CM=4-x.
在Rt△COM中,由勾股定理得:
OC2+OM2=CM2,即22+x2=(4-x)2,
解得:x=1.5,
∴M点坐标为(0,1.5).
当点C在点D左侧时,如图3,连接CM,过点A作AF⊥y轴于点F,

同理,△BAD≌△MAF,
∴BD=FM=3+x.
同理,△BAC≌△MAC,
∴BC=CM=2+x.
在Rt△COM中,由勾股定理得:
OC2+OM2=CM2,即42+x2=(2+x)2,
解得:x=3,
∴M点坐标为(0,-3).
综上,M的坐标为(0,1.5)或(0,-3).


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下三个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°.其中结论正确的结论是()

A.①②③B.①②C.①③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=4,点D为AB的中点,以点D为圆心作圆,半圆恰好经过三角形的直角顶点C,以点D为顶点,作90°的∠EDF,与半圆交于点E,F,则图中阴影部分的面积是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,B的坐标分别为(-4,5),(-2,1).

(1)写出点C及点C关于y轴对称的点C′的坐标;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,3)、B(3,-1),利用图中的“格点”完成下列作图并解答:

(1)在第三象限内找“格点”C,使得CA=CB,则点C的坐标是 ;
(2)在(1)的基础上,标出“格点”D,使得△DCB≌△ABC,则点D的坐标是 ;
(3)点M是x轴上一点,且MA-MB的值最大,则点M的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(类比概念)三角形的内切圆是以三个内角的平分线的交点为圆心,以这点到三边的距离为半径的圆,则三角形可以称为圆的外切三角形,可以得出三角形的三边与该圆相切.以此类推,如图1,各边都和圆相切的四边形称为圆外切四边形
(性质探究)如图1,试探究圆外切四边形的ABCD两组对边AB,CD与BC,AD之间的数量关系
猜想结论: (要求用文字语言叙述)
写出证明过程(利用图1,写出已知、求证、证明)
(性质应用)
①初中学过的下列四边形中哪些是圆外切四边形 (填序号)
A:平行四边形:B:菱形:C:矩形;D:正方形
②如图2,圆外切四边形ABCD,且AB=12,CD=8,则四边形的周长是 .
③圆外切四边形的周长为48cm,相邻的三条边的比为5:4:7,求四边形各边的长.
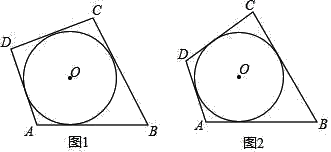
查看答案和解析>>
科目:初中数学 来源: 题型:
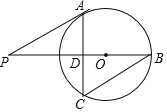
【题目】如图,已知⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C、交PB于点D,连接BC,当∠P=30°时,
(1)求弦AC的长;
(2)求证:BC∥PA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的4月23日被联合国教科文组织确定为“世界读书日”.为满足同学们的读书需某校图书室在今年“世界读书日”期间准备到书店购买文学名著和科普读物两类图书.已知20本文学名著和40本科普读物共需1520元,20本文学名著比20本科普读物多440元(注:所采购的文学名著价格都一样,所购买的科普读物的价格都一样).
(1)每本文学名著和科普读物各多少元?
(2)若学校要求购买科普读物比文学名著多20本,科普读物和文学名著总数不低于72本,总费用不超过2000元,请求出所有符合条件的购书方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com